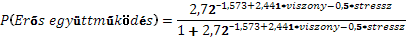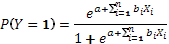Az SPSS ezen funkciója nem nagyon változott az évek során, a képen megjelölt menüpontban található a régebbi verziókban ugyanúgy, mint a mostani, legfrissebb sorozatszámú programcsomagban.

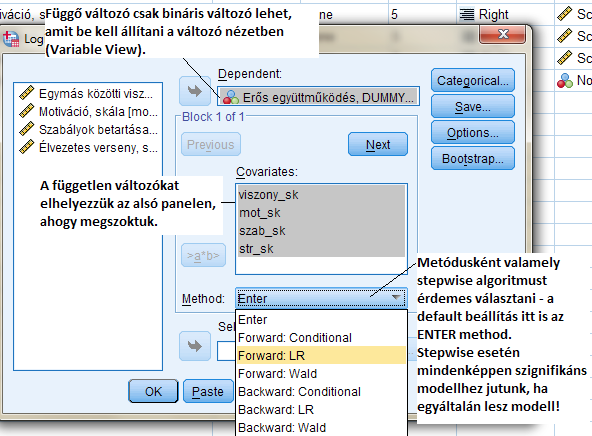
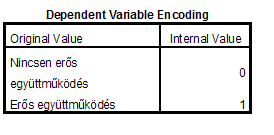
A beállítások egyszerűek, az output-elemek a következők: az első táblázatban a válaszadási arányokat, míg a második táblázatban a lehetséges kódok jelentését láthatjuk. Itt fontos megjegyezni, hogy MINDEGY, milyen eredeti kódolást használunk, mert a program saját maga számára MINDENKÉPPEN újrakódolja a bináris változót, így a kódokat innen kell leolvasnunk! Tehát az eredeti kódutasítás – kizárólag ezen elemzés erejéig – de FELÜL LESZ ÍRVA! Erre mindenképpen figyeljünk oda az értelmezés során!

Itt történik meg az újrakódolás, erre oda kell figyelni, mert az értelmezésben súlyos tévesztéseket követhetünk el, ha erről megfeledkezünk!

Az output következő néhány táblája az induló táblák közé tartozik, azaz a regresszió nélküli állapotokat írja le, így ezeken ugorhatunk addig, amíg a következő feliratot nem látjuk:

Innentől jönnek az elemzési táblázatok, ezeket fogjuk áttekinteni, értelmezni.

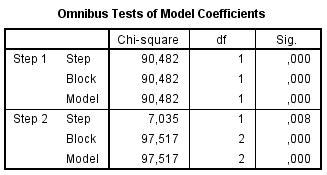
Az Omnibus-teszt a logisztikus regresszióban nem más, mint a lineáris regresszió ANOVA táblájában található, a modell szignifikáns mivoltát ellenőrző teszt analógiája. Ennek értelmében a soron következő modellünk, melyet az erős együttműködés meglétére építettünk fel, szignifikáns. Továbbá azt is láthatjuk, hogy a lépésenkénti regresszióban két lépés történik, azaz két változó kerül majd be a végső modellbe (Step 2-ig jut az algoritmus). Az output további részeiben nyilvánvaló lesz, hogy melyik két változót léptette be a program a modellbe.

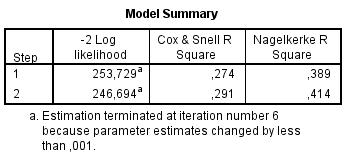
A Cox & Snell (29%), illetve Nagelkerke (41%) a determinációs együtthatók a logisztikus regresszióban, melyek közül az első nem, míg a második elvi értelemben elérheti az 1-et. (Egyes statisztikai eljárások mutatói esetében ez egy nem példa nélküli helyzet – mindkét mutatót lehet használni, itt lényegében egy korrigálásról van csak szó annak érdekében, hogy az elvileg elérhető maximum is elérhetővé váljon).

E két mutató – a determinációs együtthatók sorába illeszkedve – arról ad mértéket, hogy a modellbe került független változók hány százalékát magyarázzák a függő változó varianciájának. Mindkét mutatót szokás használni – ezek szignifikánsan nem 0-k, hiszen az Omnibus-teszt alapján szignifikáns modellt alkottunk.

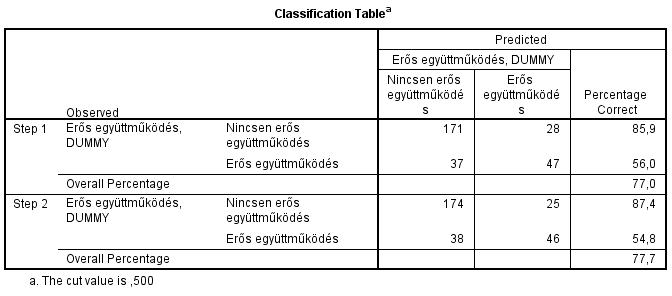
Jól látható, hogy a második lépésben megalkotott modellben a nem erősen együttműködő történetből a program 174-et jól be tudott azonosítani, a 84 erős együttműködő történetből pedig 46-ot – téves azonosítás az erős együttműködők esetében 38, míg a nem erős együttműködők esetében 25 esetben volt. A könnyebb leolvashatóság miatt, ha a bal felső/jobb alsó sarokban vannak a nagyobb számok, akkor a program „általában” jól azonosít a logisztikus regresszió segítségével.

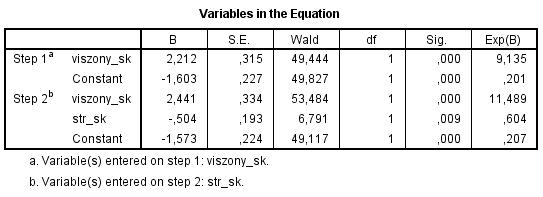
E táblázatból olvasható ki a modell, melynek formalizmusa a következő – a fenti számokat behelyettesítve, ahol a „viszony_sk” az egymás közötti viszonyt, míg a „str_sk” változó a versenyhelyzet okozta stressz mértékét jelenti:

ahol Y jelöli a függő változót (nekünk ez most az erős együttműködés, az 1-es érték pedig a fenti táblázatban, algoritmus által adott 1-es kódon lévő tulajdonság, lásd output 2. táblázata).

Az „e” szám értéke 2,72-vel helyettesíthető, az „a” érték a táblázat konstans tagja, a „b” együtthatók a táblázat B oszlopában találhatók mindig a megfelelő változóhoz kapcsoltan.