Klaszterezés ROPstat programcsomagban

A Statisztikai elemzések mintázatfeltáró elemzései között található a két klaszterezési eljárás. Hangsúlyoznánk, hogy a hierarchikus elemzésből is elérhető a k-középpontú elemzés – ezért is nem az SPSS-t mutatjuk itt be, hiszen e programban egyszerre tudjuk tárgyalni a két elemzési módot.

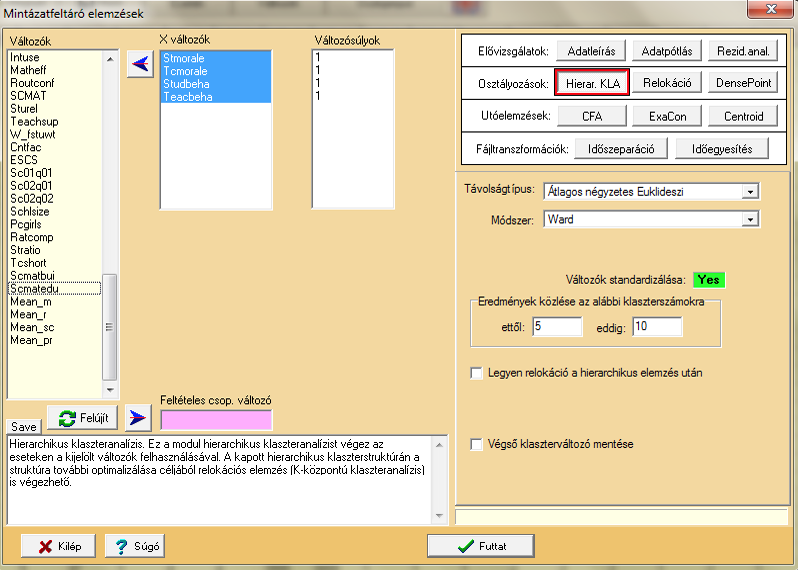
A két viselkedés- és két morál-változó alapján fogjuk a diákokat besorolni. Megadható, hogy mely eredményeket listázza a program (mi most a 3 és 4 klaszteres megoldást kérjük csak a programtól, így is elég nagy lesz a kimeneti adatok táblázata). Amennyiben kipipáljuk (márpedig érdemes), úgy a program relokációt is végez a klasztereken, ez pedig nem más, mint a k-középpontú klaszterezési eljárás.

Azaz ha 3-3 értéket adnánk meg a minimális-maximális klaszterszámnál, és kipipálnánk ezt az opciót, akkor pont a 3-középpontú klaszterezés eredményét nyernénk vele.

KLASZTERSTATISZTIKÁK 3 KLASZTERRE


Klaszter1	Klaszterkód: 1			Elemszám: 592	Homogenitási együttható: 1,19
Változó:	Stmorale	Tcmorale	Studbeha	Teacbeha
Átlag:	-0,0806	0,407	0,955	0,846
Szórás:	0,940	0,714	0,733	0,751
Min:	-1,789	-0,571	-0,750	-1,540
Max:	2,588	1,650	2,613	2,489


Klaszter2	Klaszterkód: 34			Elemszám: 324	Homogenitási együttható: 1,15
Változó:	Stmorale	Tcmorale	Studbeha	Teacbeha
Átlag:	-1,287	-0,523	-0,546	-0,300
Szórás:	0,487	0,872	0,845	0,813
Min:	-2,766	-2,179	-3,611	-2,704
Max:	0,0190	1,036	1,026	1,686


Klaszter3	Klaszterkód: 493			Elemszám: 32	Homogenitási együttható: 0,75
Változó:	Stmorale	Tcmorale	Studbeha	Teacbeha
Átlag:	1,376	1,276	-2,137	-2,013
Szórás:	0,168	0,427	0,804	0,907
Min:	1,096	0,642	-2,871	-2,704
Max:	1,637	1,650	-0,750	-0,861

A homogenitási együttható a klaszterbeli páronkénti távolságok átlaga.

Ezen a ponton túl sok magyarázni való nincsen: a klaszterekbéli átlagok, szórások találhatók a táblázatban – a homogenitási mutató segítségével pedig megfigyelhetjük, hogy a csoportok közül a 3. csoport tűnik a leginkább konzisztensnek, egységesnek – mert a homogenitási együttható itt a legkisebb, 0,75.

Silhouette mutató: SC = 0,609

A Silhouette mutató alapján tudjuk eldönteni, hogy a klaszterezés mennyire sikerült jól. 0,2 és 0,5 közötti mutatót már elfogadhatónak tart a szakirodalom, míg a 0,5 feletti mutatók általában azok, amiket kifejezetten jóként értékelhetünk – azaz jelen esetben egy kifejezetten jó osztályozást sikerült találnunk.

NEM STANDARDIZÁLT ÁTLAGOK


Klaszter	Elemszám	Stmorale	Tcmorale	Studbeha	Teacbeha
1	592	-0,0806	0,407	0,955	0,846
2	324	1,287	-0,523	-0,546	-0,300
3	32	1,376	1,276	-2,137	-2,013

A nem standardizált átlagokkal tudjuk megragadni azt, hogy mely csoport miként jellemezhető. Látható, hogy az első csoportban azok vannak, akiknél a diák- és tanár-morál értéke inkább átlagosnak nevezhető, míg a viselkedés átlaga kifejezetten magas.

A második csoportban az a 324 diák található, akiknél a két morál-érték igen alacsony – viszont a viselkedés középszerű, átlagosnak nevezhető.

A harmadik csoport esetében magas morális értékeket mutatnak mind a diákok, mind a tanárok – azonban a tanárok és diákok viselkedésének átlaga is alacsony a többi csoporthoz viszonyítva. Ez a csoport a homogenitási mutató alapján igen egységesnek nevezhető – ráadásul igen csekély létszámú is, mindösszesen 32 fő található itt. Valószínűleg e csoporttal behatóbban is megérné foglalkozni.

STANDARDIZÁLT ÁTLAGOK


Klaszter	Elemszám	Stmorale	Tcmorale	Studbeha	Teacbeha
1	592	0,35	0,32	0,54	0,47
2	324	-0,81	-0,71	-0,77	-0,63
3	32	1,76	1,28	-2,16	-2,27

A standardizált átlagok sokszor megkönnyíthetik az elemzésünket és értelmezésünket, hiszen jobban látható belőle, hogy az adott csoportok a teljes centrumtól milyen távolságra kerültek – esetünkben azonban a változók sajátosságai miatt lényegi többletinformációkat nem hordoznak.

STANDARDIZÁLT ÁTLAGOK MINTÁZATA (M = Magas, A = Alacsony)


Klaszter	Elemszám	Homog.	Stmorale	Tcmorale	Studbeha	Teacbeha
1	592	1,19	.	.	(M)	(M)
2	324	1,15	A	A	A	(A)
3	32	0,75	M+++	M+	A++++	A++++

Jelölések:

Egyszerű kiírás: 0,675 <= |z| <= 1,000 (p: 16-25%)

( ): 0,44 <= |z| <= 0,674 (p: 25-33%)

+: 1,001 <= |z| <= 1,404 (p: 8-16%)

++: 1,405 <= |z| <= 1,644 (p: 5-8%)

+++: 1,645 <= |z| <= 2,044 (p: 2-5%)

++++: 2,045 <= |z| (p: 0-2%)

Az előző megállapítások egy összefoglaló táblázatban is megtalálhatók: itt jól megfigyelhető, hogy a harmadik csoport igen markánsan elkülönül a többi csoporttól, a morál szignifikánsan magas, míg a viselkedés szignifikánsan alacsony volta drasztikusan megkülönbözteti e csoport 32 tagját lényegében az egész populációtól.

Ráadásul alább láthatjuk azt is, hogy a megmagyarázott variancia-aránya e csoportba sorolásnak igen magas (gondoljunk bele abba, hogy 3 értékkel, 3 klaszterrel 4 változó viselkedését foglaljuk össze úgy, hogy az ebből származó magyarázott variancia-arány 42%-os).

Total ESS = 3788,00 Aktuális ESS = 2189,90 Megmagy.ESS% = 42,19

Érdemes megvizsgálnunk azonban, hogy a hierarchikus klaszterezéssel készített csoportba bontás mennyire stabil – ennek érdekében pedig relokációt végzünk. Hiszen ha stabil állapotot mutat ez a csoportba sorolás, akkor érdemi eltérést (K-középpontú klaszterezéssel) nem lenne szabad tapasztalnunk akkor, amikor megpróbáljuk stabilabb, újraszervezett rendben megvizsgálni a 3 klaszter egymáshoz való viszonyát (terjedelmi okokból nem nézzük a 4-es bontást, az értelmezése ehhez hasonló, gyakorlásként mindenkinek javasoljuk, hogy a 4 klaszteres eredményeket vizsgálja meg önállóan feldolgozandó munkaként).

RELOKÁCIÓ: K-központú klaszteranalízis 3 klaszterrel

Teljes ESS = 3788,00 Aktuális ESS = 2189,90 Megmagyarázott ESS% = 42,19


Iterációs sorszámm	Áttett esetek	ESS	Megmagy ESS %	Pontbiszeriális együttható
i=1	123	2057,05	45,70	0,465
i=2	28	2023,55	46,58	0,469
i=3	12	2021,67	46,63	0,469
i=4	0	2021,67	46,63	0,469

Jól látható, hogy jó pár átsorolás történik, aminek segítségével ugyan nem jelentős mértékben, de javítani lehet a magyarázott variancia-arányon (42-ről 46,47%-ra).

__________________________________________

VÉGSŐ KLASZTERSTATISZTIKÁK 3 KLASZTERRE

KLASZTER 1 Elemszám: 475 Homogenitási együttható: 1,13


Változó:	Stmorale	Tcmorale	Studbeha	Teacbeha
Átlag:	0,0823	0,634	1,063	0,936
Szórás	0,938	0,621	0,745	0,771
Min:	-1,789	-0,571	-0,750	-0,861
Max:	2,588	1,650	2,613	2,489

KLASZTER 2 Elemszám: 419 Homogenitási együttható: 0,94


Változó:	Stmorale	Tcmorale	Studbeha	Teacbeha
Átlag:	-1,144	-0,565	-0,161	0,0013
Szórás	0,579	0,723	0,771	0,727
Min:	-2,766	-2,179	-2,477	-1,760
Max:	1,096	0,642	1,386	1,686

KLASZTER 3 Elemszám: 54 Homogenitási együttható: 1,53


Változó:	Stmorale	Tcmorale	Studbeha	Teacbeha
Átlag:	0,362	0,891	-2,171	-1,955
Szórás	1,268	0,647	0,834	0,756
Min:	-1,789	-0,571	-3,611	-2,704
Max:	1,637	1,650	-0,750	-0,861

Vegyük észre, hogy az előző kimenethez képest a homogenitási együtthatók jelentős mértékben megváltoztak, most a harmadik klaszternek lett a legnagyobb a homogenitási együtthatója. Az átrendezésnek tehát valóban érzékelhető, számításokkal alátámasztható hatása jelentkezett.

A homogenitási együttható a klaszterbeli páronkénti távolságok átlaga.

Silhouette mutató: SC = 0,646

Megfigyelhető, hogy a klaszterezettség mértéke javult valamelyest – azonban a klaszterek homogenitása némiképpen átrendeződött. A leíró statisztikákból már láthatók az átlagok, tehát az elsődleges jellemzőket megalkothatjuk már ebből is. Ahogy az előzőekben is, úgy most is megadja a program a standardizált és nem standardizált átlagokat, melyek segítségével jobban átláthatjuk, hogy történt-e valami lényeges változás az előző, hierarchikus elemzésekhez képest. Nyugtázhatjuk azonban, hogy a számunkra leginkább érdekes 3-as klaszter érdemi változásokon nem ment át – azonban a másik két klaszter az egyértelműen MAGAS és ALACSONY értékek klaszterévé vált.

NEM STANDARDIZÁLT ÁTLAGOK


Klaszter	Elemszám	Stmorale	Tcmorale	Studbeha	Teacbeha
1	475	0,0823	0,634	1,063	0,936
2	419	-1,144	-0,565	-0,161	0,0013
3	54	0,362	0,891	-2,171	-1,955

STANDARDIZÁLT ÁTLAGOK


Klaszter	Elemszám	Stmorale	Tcmorale	Studbeha	Teacbeha
1	475	0,51	0,57	0,63	0,55
2	419	-0,68	-0,75	-0,44	-0,34
3	54	0,78	0,85	-2,19	-2,21

STANDARDIZÁLT ÁTLAGOK MINTÁZATA (M = Magas, A = Alacsony)


Klaszter	Elemszám	Homog.	Stmorale	Tcmorale	Studbeha	Teacbeha
1	475	1,13	(M)	(M)	(M)	(M)
2	419	0,94	A	A	(A)	.
3	54	0,53	M	M	A++++	A++++