Hagyományosan két értéket fogunk figyelni. A legalsó Sig-érték megmutatja, hogy e változó-szett szignifikánsan eltér-e a teljesen független változók struktúrájától (azaz ha a Sig-érték 0,05 alatt van, akkor a változóink nem teljesen függetlenek egymástól). Továbbá a KMO-érték 0,5 feletti – általában 0,7 és 0,8 közötti értékeknél lennénk elégedettek, de ez a 0,634 is kellő reményt szolgáltat ahhoz, hogy valamely látens struktúrára bukkanjunk.

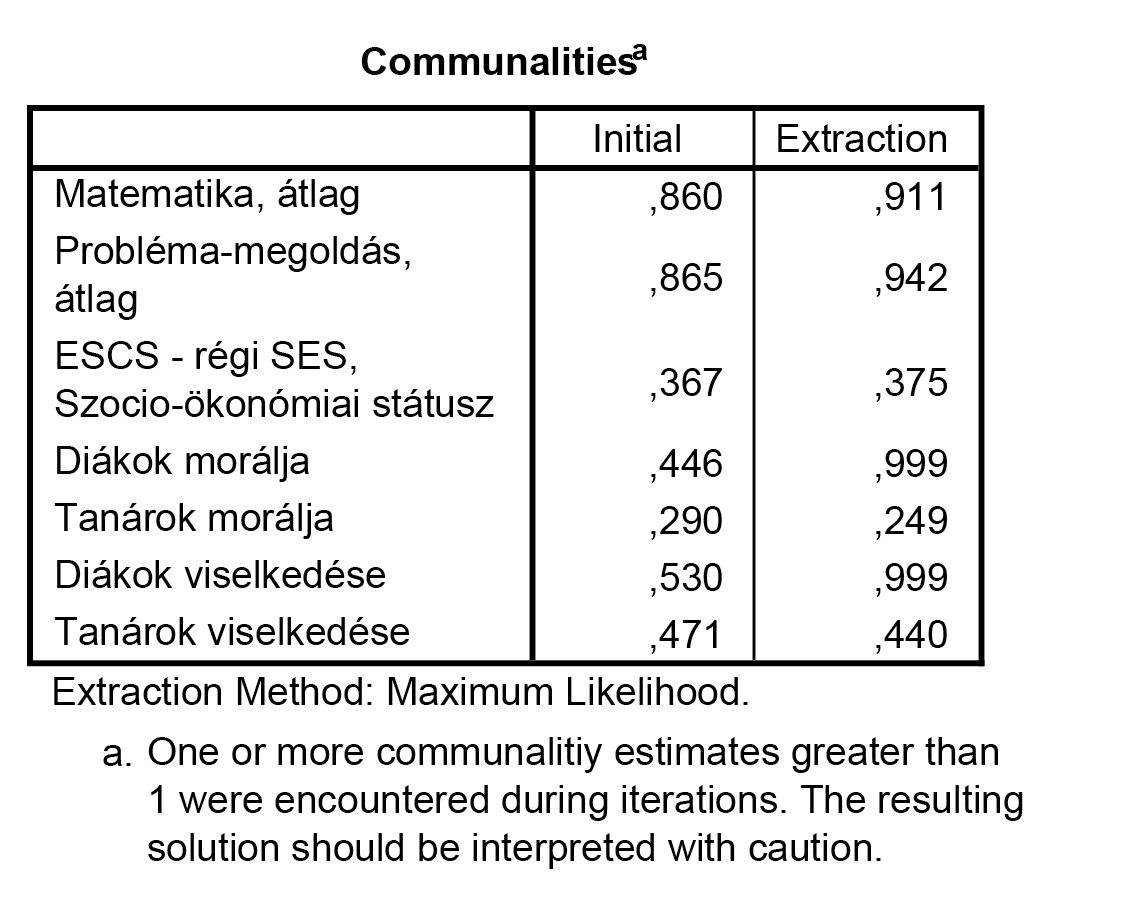
A kommunalitások megmutatják, hogy a végső modellben milyen magyarázóerővel bírnak az egyes változók (úgy is értelmezhetjük, hogy az adott változó varianciájából a közös faktormodell mekkora hányadot magyaráz). Ha van forgatás, akkor általában az Extraction oszlop értékeit figyeljük. (Az első oszlopban azt látjuk, hogy a többi változó mennyit magyaráz az adott változóból. Ez az adott itemnek az összes többi itemmel vett többszörös korrelációja). Az Extraction oszlopban 0,25-nél alacsonyabb értékekkel bíró változók elhagyhatók (hiszen a teljes modell varianciáját nézve nem magyaráznak túl sok mindent). Jelen esetben a tanárok morálja változó majdnem ezen az értéken található, de miután csak 1 ezreddel marad el a minimálisan elvárttól, nem futtatjuk újra a modellt, hanem megpróbáljuk így értelmezni.

Ha mégsem így döntünk, akkor a változó-szetthez visszalépve a menüben, onnan kiemelve ezt, újra kell futtatnunk az eljárást egészen addig, amíg minden változó végső kommunalitása el nem éri a megkívánt 0,25-ös értéket.

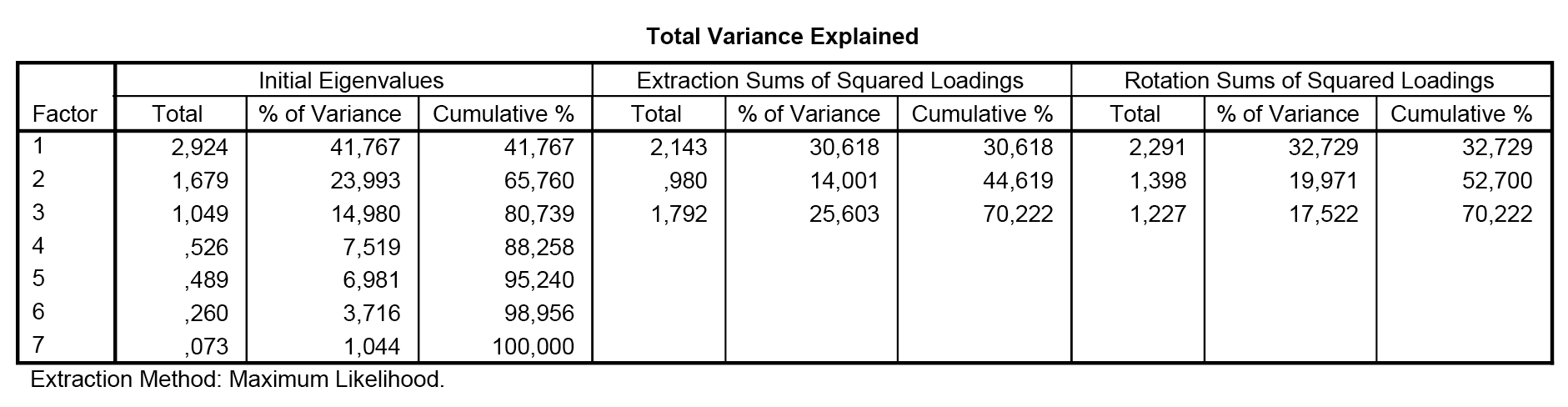
A sajátértékek táblázatából több mindent is leolvashatunk. Az egyik az utolsó oszlop legalsó száma: 70,222%-os értékével azt mondja, hogy ha a 7 változó helyett a 3 faktorváltozót használjuk (tehát a megtalálható háttérváltozókat), úgy a változókban rejlő információ 70%-át meg tudjuk őrizni. Ha figyelembe vesszük, hogy a változók számát megfelezve az információnak a 70%-a megmarad, úgy ezt egy jó modellnek tekinthetjük (általában 30%-os határt minden modellnél illik elérni, bizonyos helyzetekben akár az 50% is megkövetelhető).

Nézzük meg továbbá, hogy a program betartotta az 1-es sajátértéknél való vágást (első oszlop), hiszen 3 sajátérték van 1 felett, e három sajátértékhez rendelt faktort a program. Továbbá a két hátsó blokkban megfigyelhetjük, hogy a rotáció kicsit kiegyensúlyozta a magyarázó erőket a változók között – a második változó magyarázó erejét („% of Variance” oszlop) kissé megemelte a harmadik kárára.

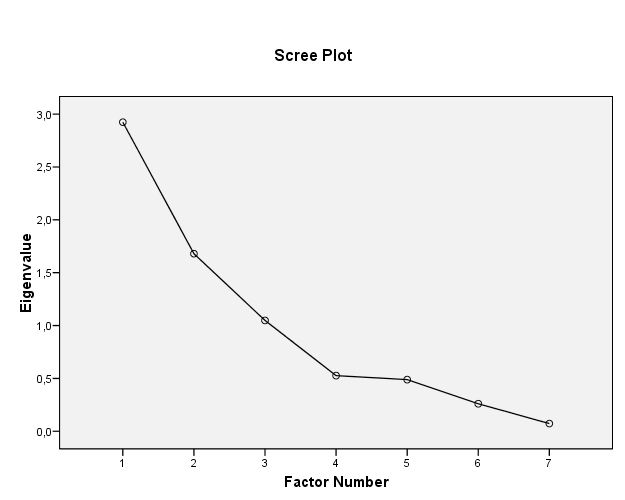
A Scree Plot grafikonja segít annak megállapításában, hogy hol van érdemi törés a sajátértékek görbéjén. Így itt azt is leolvashatjuk, hogy hány faktoros modellt célszerű készíteni. Miután a fenti modellben a 4. sajátértéknél válik igazán lankássá a görbe, így akár jogosnak is vehetjük, hogy 3-nál már megálltunk. De ne feledjük, hogy ezen ábra alapján a 4 faktoros modellnek is lehetne létjogosultsága (gyakorlásképpen futtathatjuk azt az opciót is, és megpróbálhatjuk értelmezni az eredményeket).

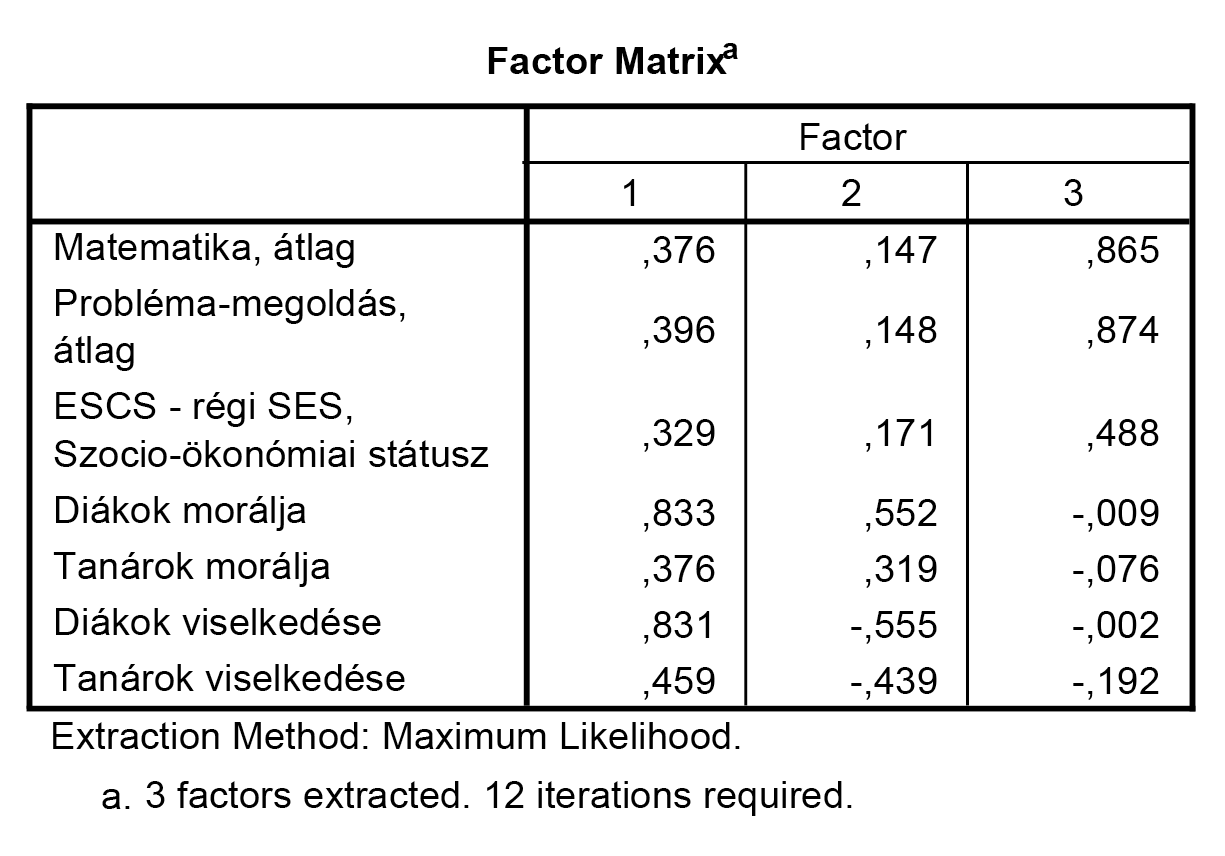
A faktor mátrixra akkor van szükségünk, ha a rendszerben nincsen rotáció. A rotált és a faktor mátrix értelmezése azonos, de hangsúlyozzuk: ha van rotáció, akkor a rotált eredményeket nézzük, hiszen pont az interpretáció megkönnyítése érdekében kértünk forgatást a programtól.

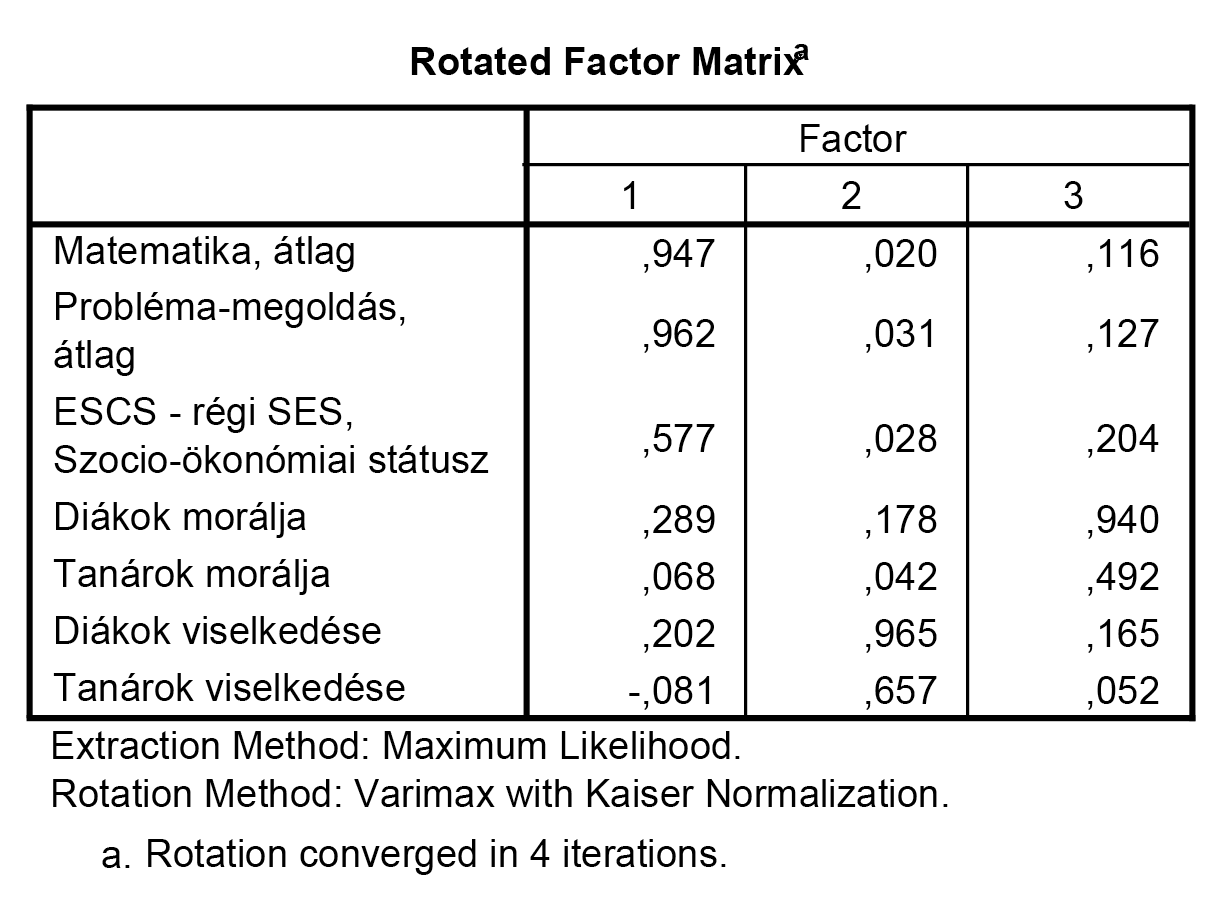
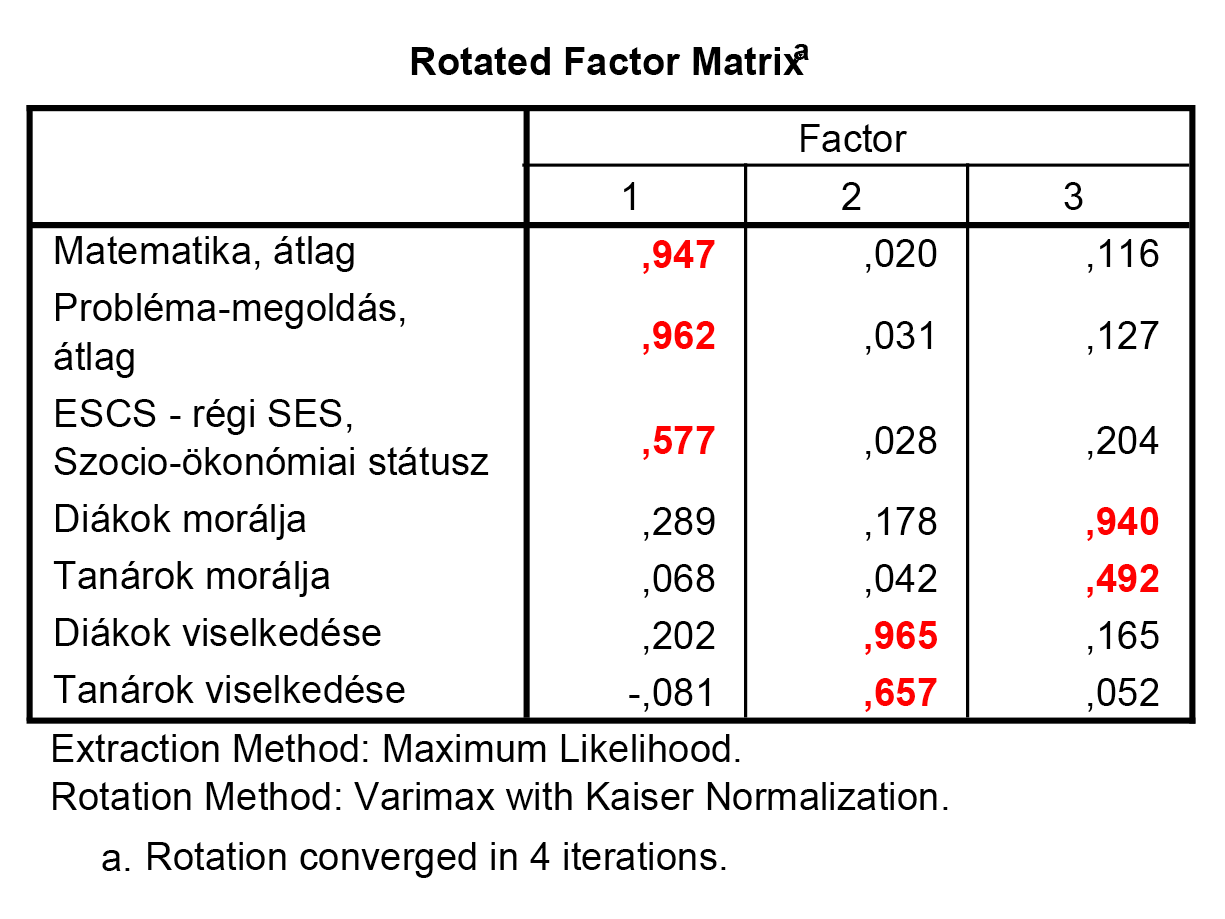
A változókat úgy értékeljük, hogy kétszer végignézzük a táblázatot. Először soronként megnézzük, hogy mely változó mely faktoron szerepel a legnagyobb abszolút értékű súllyal. Ha ez a súly nagyobb, mint bármely más faktoron lévő súly másfélszerese (sőt, dolgozhatunk kétszeres értékkel is), akkor azt a változót ahhoz a faktorhoz rendeljük. Ha nem nagyobb, akkor megyünk tovább a súlyokban, és a változót a „nagy súlyokkal képviselt” faktorokhoz rendeljük. Így az alábbi ábrát készíthetjük el:

Megfigyelhető, hogy az első faktoron a teljesítmény-változók és az otthoni háttér változója található (megállapítható, hogy ez valahol a diák és a szülők teljesítményét foglalja össze, ha úgy tetszik, egyfajta családi teljesítménybéli háttérként értelmezhető).

A második faktoron a diákok és tanárok viselkedése található, a harmadik faktoron pedig a diákok és tanárok morálja. Vegyük észre, hogy a már vizsgált tanárok morálja változó nem túl nagy súllyal szerepel a hármas faktoron (ezért is lehet akár jogos e változó kivétele az elemzésből).

Továbbá azt is észrevehetjük, hogy – bár igen kis súllyal – a tanárok viselkedése ellentétes a diákok teljesítményével, hiszen negatív értékkel szerepel a faktoron. Más megközelítésben: a tanárok szigora, távolságtartóbb magatartása (ridegebb viselkedése) bizonyos helyzetekben növelheti a diákok teljesítményét – hiszen ellentétes előjelet mutat a változó a teljesítmény-faktoron. Jegyezzük azonban meg, hogy ez egy hatalmas rendszer, melyből most kiragadtunk változókat – tehát a fenti értelmezés és megfogalmazás azon kritériumok mentén érvényes csak, hogy ha e változókkal és CSAK e változókkal rendelkező világot szemlélünk.

Figyeljünk oda arra, hogy ha megszabadulnánk is egy-egy változótól, egyszerre mindig csak 1 változót szedjünk ki az elemzésből, hiszen egyes változók kivétele teljesen megbolygatja a struktúrát! Továbbá jegyezzük meg azt is, hogy e fenti szett esetén tudtunk jelentést adni a faktoroknak, azonban ha olyan faktormodellt csinálunk, mely „csak illeszkedik”, de a változók rendszerét nem tudjuk szakmai tartalommal megtölteni, akkor érdemi munkát nem nagyon végeztünk.