Rangsorolásos eljárás alkalmazása

Rangsorolásos eljárás alkalmazása
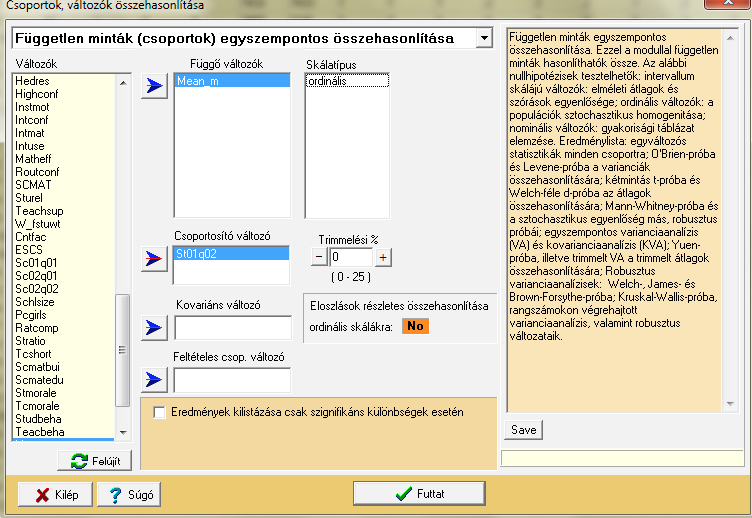
Amennyiben úgy véljük, hogy a normalitás sérül, és az esetszám is alacsony (tehát a varianciaanalízis megbízhatósága jelentősen lecsökken az előfeltételek sérülése miatt), úgy a robusztusabb rangstatisztikai eljárások felé mozdulhatunk el. Ehhez annyit kell csak tennünk, hogy a függő változónk skálatípusát intervallum-típus helyett ordinálisra állítjuk.
A kimeneti adatok hasonlatosak a rangstatisztikák esetén is.
Csoportonkénti alapstatisztikák
| Sztochasztikus Dominancia | ||||||
| Index | St01q2 | Esetek | Rang-átlag | Rang-szórás | Súlyozott | |
| 1 | 1 | 92 | 224,89 | 187,82 | 0,224 | 0,302 |
| 2 | 2 | 335 | 720,54 | 218,25 | 0,720 | 0,782 |
| 3 | 3 | 381 | 505,11 | 237,56 | 0,505 | 0,595 |
| 4 | 4 | 192 | 239,49 | 184,07 | 0,239 | 0,322 |
Megjegyzés:
Minden csoport esetében a sztochasztikus dominancia annak a valószínűségét jelzi,
hogy egy random megfigyelés ebből a csoportból (Xj) nagyobb lesz, mint egy random
megfigyelés az egész mintából (X), plusz az egyenlőség valószínűségének a fele:
SZTDj = P(Xj > X) + 0,5P(Xj = X)
A sztochasztikus homogenitás definíciója: SZTD1 = SZTD2 = SZTD3 = ... = 0,50
Emlékeztetnénk: a sztochasztikus dominancia azt mondja, hogy ha véletlenszerűen választanánk egy egyedet valamely csoportból, illetve véletlenszerűen választanánk bármely más csoportból, úgy igaz-e az, hogy a vizsgált csoportból származó egyed nagy valószínűséggel nagyobb értéket mutat, mint a bárhonnan máshonnan választott vizsgálati egyed. (Hangsúlyoznánk, hogy az is szignifikáns eltérés, ha szisztematikusan alacsonyabb értékeket mutat – bár ekkor a dominancia kifejezés némiképpen félrevezető lehet.)
Elméleti rangszórások egyenlőségének tesztelése
- O’Brien-próba (Welch-féle): F(3,0; 338,8) = 8,384 (p = 0,0000)***
- Levene-próba (Welch-féle): F(3; 347,2) = 9,373 (p = 0,0000)***
Megállapíthatjuk, hogy a rangszórások szignifikánsan különböznek egymástól (azaz sérül az elméleti rangszórások egyenlősége) – tehát itt nem hagyatkozhatunk a hagyományos tesztre, hanem majd robusztus összehasonlításokat kell figyelnünk.
Sztochasztikus homogenitás tesztelése
Hagyományos eljárás, amely feltételezi a szóráshomogenitást:
- Kruskal-Wallis-próba: H(3) = 435,126 (p = 0,0000)***
A szóráshomogenitás sérülése miatt a második, korrigált rang Welch-próbát figyeljük, mely alapján állíthatjuk, hogy szignifikáns eltérések vannak a rangátlagok között – sztochasztikus homogenitás nem áll fenn.
Szóráshomogenitást nem igénylő robusztus közelítő eljárás:
- Korrigált rang Welch-próba: rW3(3; 352,0) = 301,348 (p = 0,0000)***
KULLE-féle aszimptotikusan egzakt próbák
- Populációk azonos súlyozása:
Khi2(2,13) = 554,613 (p = 0,0000)*** F(2,13; 667,4) = 260,317 (p = 0,0000)***
- Mintaelemszámokkal arányos súlyozás:
Khi2(2,40) = 729,041 (p = 0,0000)*** F(2,40; 651,0) = 303,540 (p = 0,0000)***
Elemezhető itt is a rangsorok páros összehasonlítása (a Bonferroni-teszt mindenképpen robusztus teszt, tehát ennek hihetünk – talán túlságosan is robusztus).
Ezek ugyanazt az eredményt mutatják, mint a hagyományos eljárás eredményei: csak az 1. és 4. csoport, azaz az általános iskola és szakiskola között nincsen eltérés.
Az egyes csoportok összehasonlítása a teljes minta többi részével a Brunner-Munzel-próba segítségével.
A p-értékeket a Bonferroni-módszerrel korrigáltuk.
| Index | Csoport | A becsl. | BM | szab.fok | p-érték | korrigált p |
| 1 | 1 | 0,196 | -14,78 | 130,7 | 0,0000 | 0,0000*** |
| 2 | 2 | 0,831 | 24,94 | 714,8 | 0,0000 | 0,0000*** |
| 3 | 3 | 0,507 | 0,41 | 992,6 | 0,6799 | 1,0000 |
| 4 | 4 | 0,177 | -22,22 | 419,6 | 0,0000 | 0,0000*** |
Páronkénti sztochasztikus egyenlőség tesztelése
| A(1,2) = 0,062 BM(154,6) = -33,266 | (p=0,0000) | Bonferroni szignif.: p=0,0000*** |
| A(1,3) = 0,179 BM(140,9) = -13,393 | (p=0,0000) | Bonferroni szignif.: p=0,0000*** |
| A(1,4) = 0,469 BM(182,0) = -0,844 | (p=0,3988) | Bonferroni szignif.: p=1,0000 |
| A(2,3) = 0,751 BM(680,9) = 13,869 | (p=0,0000) | Bonferroni szignif.: p=0,0000*** |
| A(2,4) = 0,937 BM(481,7) = 43,162 | (p=0,0000) | Bonferroni szignif.: p=0,0000*** |
| A(3,4) = 0,807 BM(419,9) = 16,781 | (p=0,0000) | Bonferroni szignif.: p=0,0000*** |