Vizsgakérdések – többszörös lineáris regresszió

	I	H
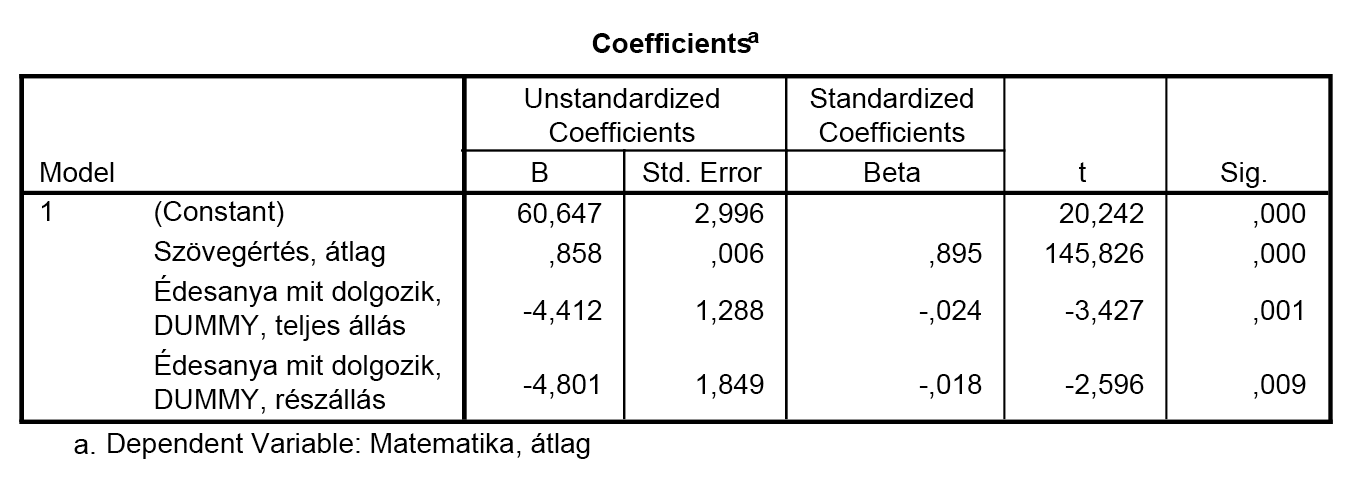
A B-értékek alapján a konstans tagnak van a legnagyobb hatása a függő változóra.		X
A Beta-értékek segítségével állapítható meg, hogy melyik változónak milyen mértékű hatása van a függő változóra – a többi változóhoz képest.	X
A fenti elemzésben az output alapján lépésenkénti regressziót alkalmaztunk.		X
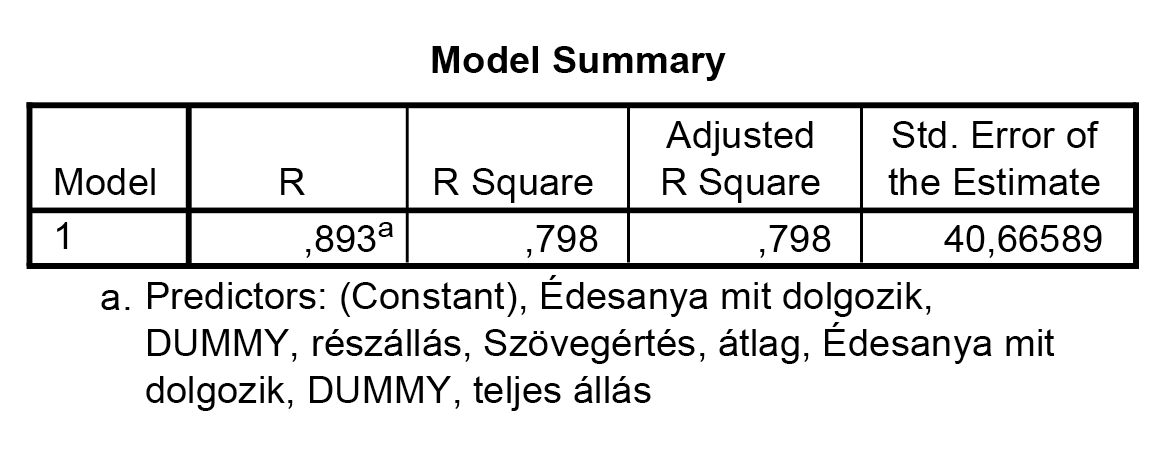
A magyarázott variancia-arány 89,3%-os.		X
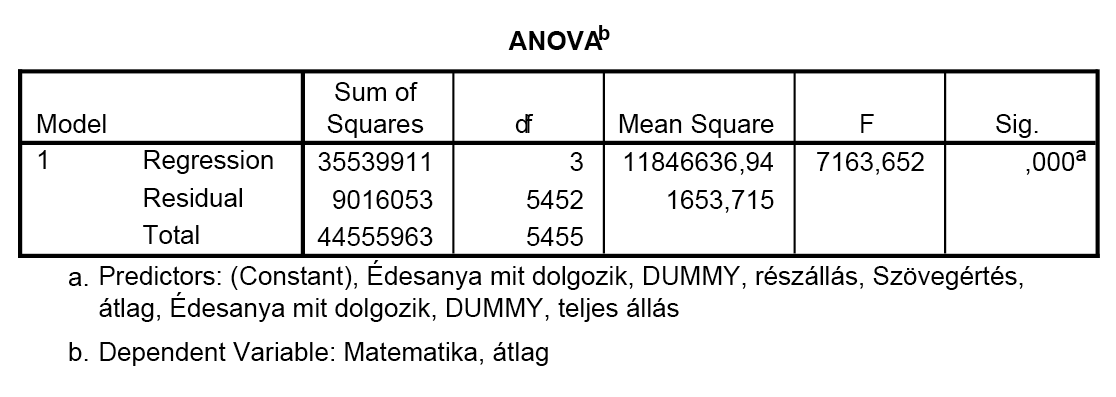
Az ANOVA táblázatból megtudható, hogy a magyarázott variancia-arány, illetve a korrelációs együttható szignifikánsan különbözik-e 0-tól.	X
Az együtthatók táblázatában látható t-érték azt mutatja meg, hogy az adott változó 0 vagy nem 0.		X
Minél nagyobb a reziduális, annál pontosabb a becslés.		X
A lineáris regresszió esetén az eredeti négyzetösszeget bontjuk fel a regresszió által magyarázott négyzetes eltérés összegére és a reziduálisra.	X
Ha az ANOVA táblázatban a SIG-érték 0,05 alatt van, érvényes modellt alkottunk.	X
A determinációs együttható maximuma 1, minimuma -1, mely értékeket függvényszerű kapcsolat esetén érhetünk el.	X
A korrelációs együttható a determinációs együttható négyzete.		X
A magyarázó változók esetében az a jó, ha azok egymással minél szorosabban összefüggnek – így építhető erős és jól magyarázható lineáris modell a függő változóra.		X
Minden diszkrét változó átalakítható DUMMY változóvá.	X
Az együtthatók táblázatának t-értéke és hozzá tartozó szignifikancia arról tájékoztat minket, hogy az adott magyarázó változó együtthatója 0 vagy nem 0 a lineáris regresszió egyenletében.	X
A DUMMY változóknak mindig 2 értéke van.	X

Magyarázatok – az igaz válaszokat nem magyarázzuk, csak a hamis válaszok esetén adunk segítséget azok értelmezésében, mely szokásunkat végig megőrizzük.

1. A B-értékek alapján a konstans tagnak van a legnagyobb hatása a függő változóra.

2. A fenti elemzésben az output alapján lépésenkénti regressziót alkalmaztunk.

3. A magyarázott variancia-arány 89,3%-os.

4. Az együtthatók táblázatában látható t-érték azt mutatja meg, hogy az adott változó 0 vagy nem 0.

5. Minél nagyobb a reziduális, annál pontosabb a becslés.

6. A korrelációs együttható a determinációs együttható négyzete.

7. A magyarázó változók esetében az a jó, ha azok egymással minél szorosabban összefüggnek – így építhető erős és jól magyarázható lineáris modell a függő változóra.

A B-értékek nem erre szolgálnak. Az a lineáris regresszió egyenletében az együtthatók értékei, azaz az adott változó egységnyi növelése esetén – és a többi magyarázó változó helyben maradásakor – azt jelentik, hogy várhatóan mekkora változás áll be a függő változóban. Ráadásul a konstans tag pusztán a tengelymetszet, mely nem más, mint az összes magyarázó változó 0 volta esetén a függő változóra vonatkozó becslés, így ennek „legnagyobb hatása” nem is lehetséges.
A lépésenkénti regressziót ebből a három táblázatból nem tudhatjuk. Sehol nincsen jelzés arra vonatkozóan, hogy milyen típusú regressziós technikát alkalmaztunk.
A többszörös korrelációs együttható volt 0,893, a magyarázott variancia-arány, vagy determinációs együttható ennek négyzete, 0,798 volt.
A t-érték jelentése a változó együtthatójára, nem a változóra vonatkozik. Még csak nem is a változó átlagára, mint az egymintás t-próba esetén.
Minél kisebb a reziduális, annál kisebb a hiba, tehát annál pontosabb a becslés.
A determinációs együttható gyöke a korrelációs együttható abszolútértéke, tehát a megfogalmazás fordítva igaz.
A magyarázó változók szoros kapcsolata úgynevezett multikollinearitást hoz létre, aminek hatására a magyarázó változók redundáns információkat tartalmaznak, így mind az interpretálásuk, mind a magyarázó készségük gyengül. Gondoljunk az értelmezésnél arra, hogy az együtthatókat éppen úgy értelmezzük, hogy az adott változó egységnyi megváltozására – ha minden más változó helyben marad – várhatóan mennyit változik a függő változó. Azonban a „minden más helyben marad” feltételt nehéz akkor teljesíteni, ha a magyarázó változók között erős összefüggések vannak.