Az SPSS programcsomagban is általában úgy készítjük el a modelleket, hogy váltogatjuk a struktúrákat, lényegében próbálgatjuk a lehetséges modelleket.

Tekintsük a szondi_m.sav adatállományt, mely a ROPstat programcsomag azonos nevű adatállományának SPSS-be átkonvertált állománya. Ebben az állományban nemre, korra és iskola végzettségre való bontását láthatjuk a mintának. Jogosan felmerülhet a kérdés, hogy a nem, kor és iskolai végzettség szerinti válogatás teljesen véletlenszerűen történt-e, vagy pedig valamely rejtett összefüggések feltételezhetők. A fenti változók kategória-változók, tehát a különböző regressziós modellek nem alkalmazhatók rájuk.

A nem-kor-iskolai végzettség (isk) hármasban tehát az alábbi kombinációk lehetnek.

A lehetséges figyelembe vehető változó-kombinációk: nem, kor, isk, nem-kor, nem-isk, kor-isk, nem-kor-isk, azaz adott az első három marginális, a 3 darab kettes interakció és az egyetlen hármas interakció. Világos az is, hogy amennyiben a modellben mindegyik most említett kombinációt felsoroljuk, úgy egy teljesen illeszkedő modellt nyerünk (ahogy a fenti dohányzó−nem dohányzó, nemek szerinti bontásban, ha megadtuk lényegében a teljes együttes eloszlást), a cél tehát az, hogy valamilyen módon ezt az összesen 7 „változót” lecsökkentsük oly módon, hogy egy elfogadható szintű illeszkedést nyerjünk.

Az illeszkedést khi-négyzet próbával fogjuk majd ellenőrizni.

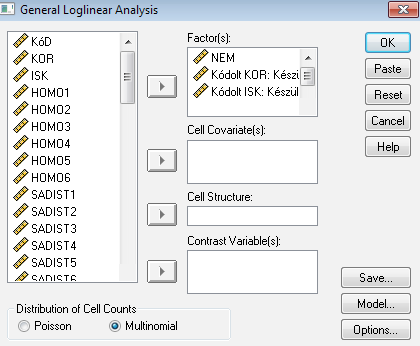
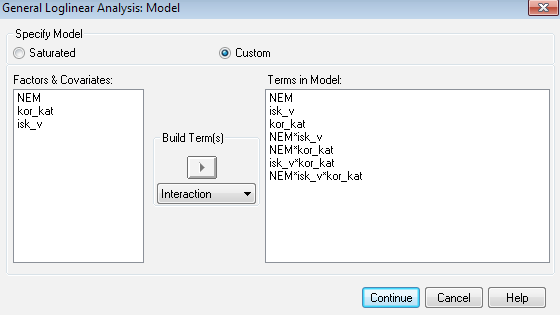
Az általános modellben fogunk dolgozni, melybe elhelyezzük az összes változót.

A változókat elhelyezzük, és alapvetően úgy gondoljuk, hogy a változóink egymástól függetlenek (nincs okunk feltételezni ennek ellenkezőjét). A Model… gombra nyomva tudjuk megadni, hogy mely interakciókat vegyük figyelembe és melyeket nem. Két eltérő outputot mutatunk be annak érdekében, hogy látszódjon: mely kimenetel esetén láthatjuk, hogy az elkészített modellünk egészen biztosan nem illeszkedik a tapasztalt gyakoriságokhoz – és mely eset az, amikor valamifajta illeszkedést elértünk, és innentől lényegében „kutatói szabadságunk és vérmérsékletünk” befolyásolja, hogy elfogadjuk-e a modellünket, vagy további interakciókat építünk még be. Bemutatjuk azt is, hogy amennyiben minden interakciót beépítünk, úgy lényegében egy „felesleges” modellt nyerünk – egy modellt akkor tekintünk e terminológiában feleslegesnek, ha érdemi információt nem közöl, és amint azt látni fogjuk, ez fog majd történni.

Az első modell

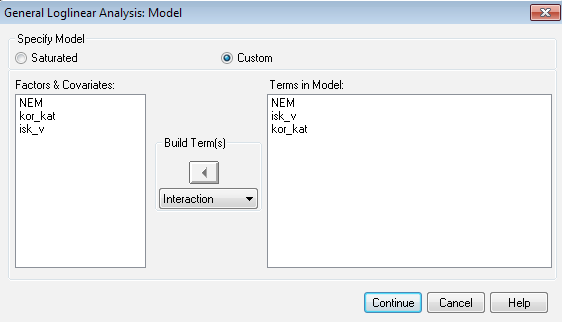
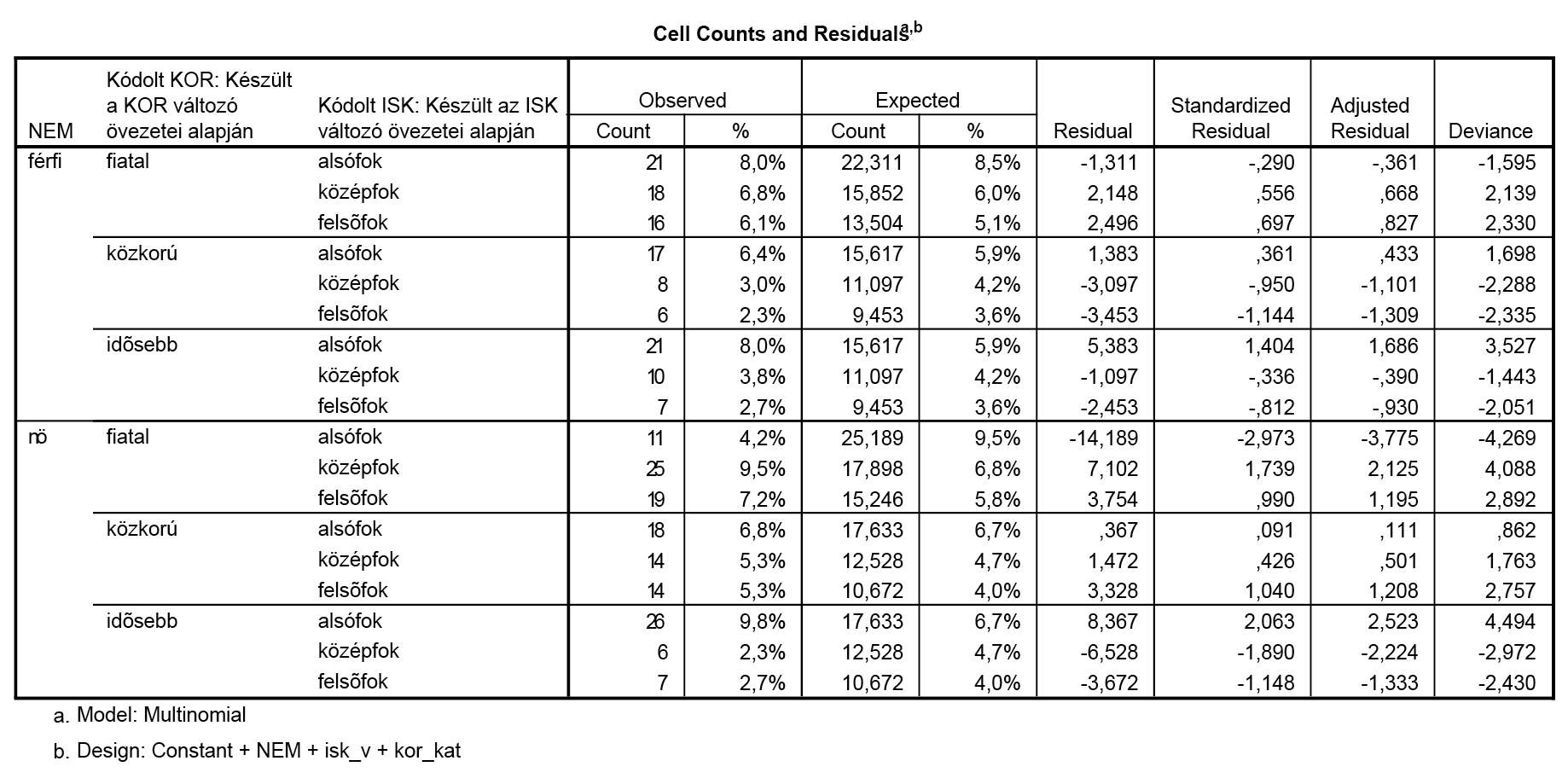
Látható, hogy itt most egyetlen interakciót sem veszünk figyelembe, hanem kizárólag a 3 marginálissal szeretnénk modellezni. Ez lényegében az az eset, amikor a teljes függetlenség áll fenn, hiszen ilyenkor tudnánk azt elérni, mely a fentiek szerint az együttes bekövetkezés valószínűségét a marginálisokkal tudja kezelni.

Jól látható, hogy a modell egyáltalán nem illeszkedik a tapasztaltakhoz, azaz pusztán a marginálisok figyelembe vételével nem tudunk jó illeszkedést elérni.

A második modell

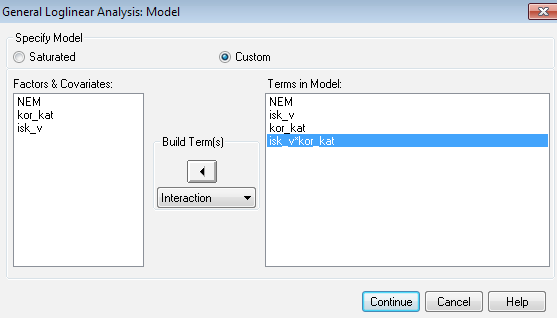
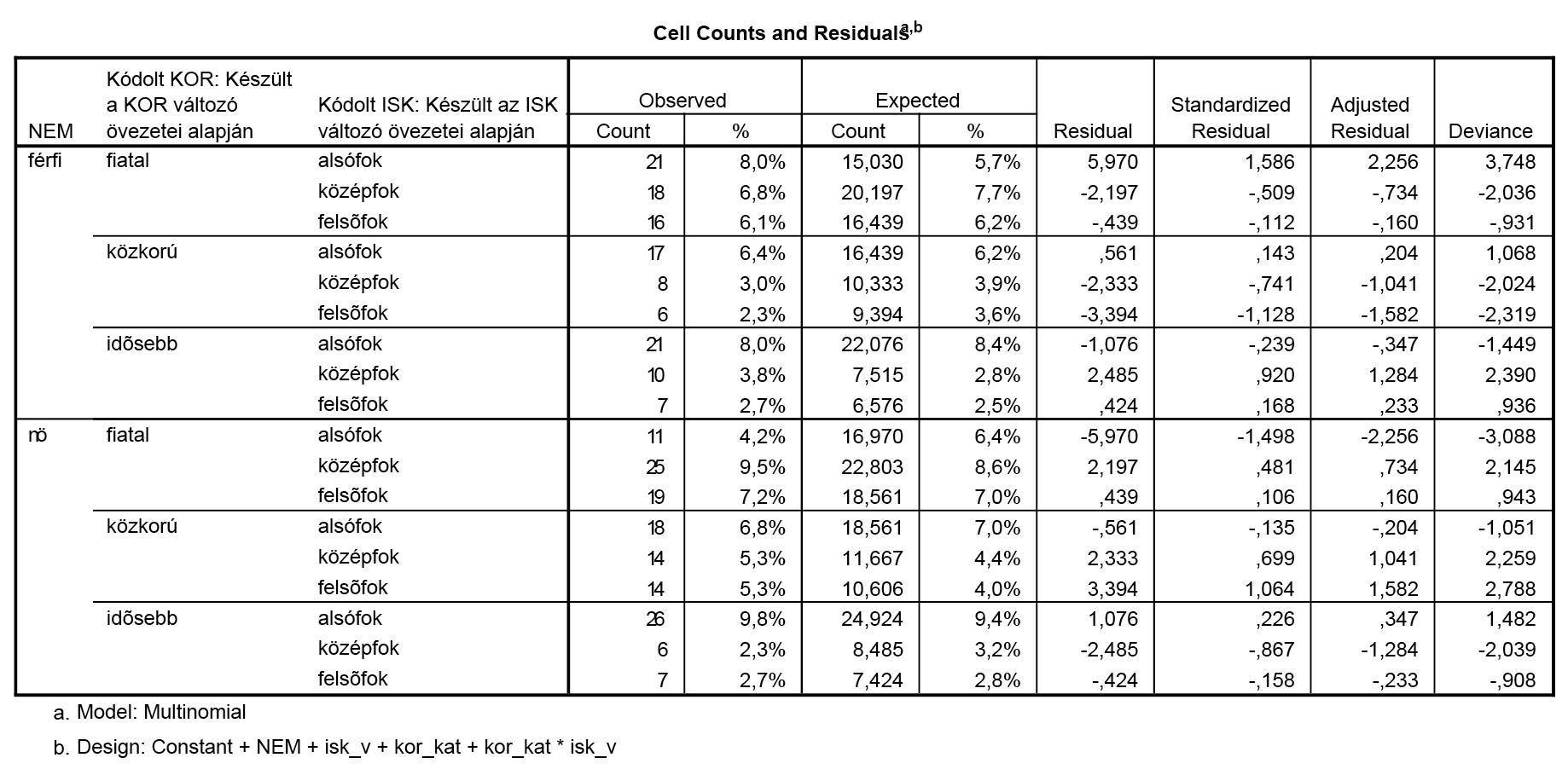
Kijelölve az iskolai végzettség és a korkategória változókat, azok interakcióját is beépíthetjük a modellbe. Amennyiben ezt a változatot választjuk, úgy az alábbiakat nyerjük:

Jól látható, hogy lényegesen jobb illeszkedést tudtunk elérni.

Az első és második modell összehasonlítása

Amennyiben a modellt leíró cellánkénti eltéréseket összehasonlítjuk, úgy a két modellben megfigyelhető, hogy összességében valóban kevesebb eltérést tapasztalunk (a reziduálisok a második modellben lecsökkentek).

Míg az első modellben a nők esetében több, 10 körüli (vagy akár 10-nél nagyobb) eltérés is tapasztalható volt, addig a második esetben minden eltérés 6 alatti, tehát a cellák gyakoriságainak nagy részét legfeljebb 6-os eltéréssel sikerült megadnunk.

A harmadik – semmitmondó – modell

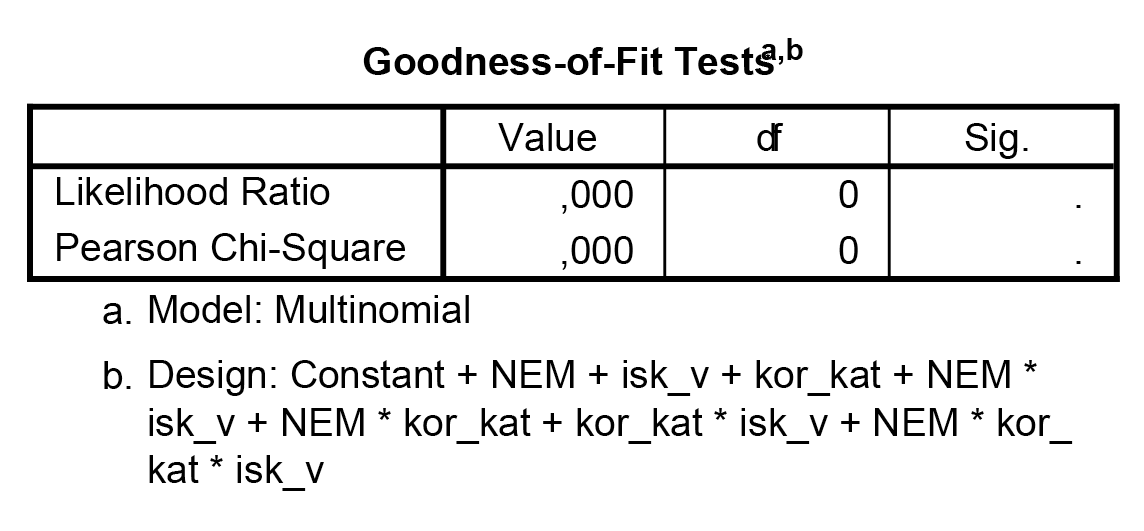
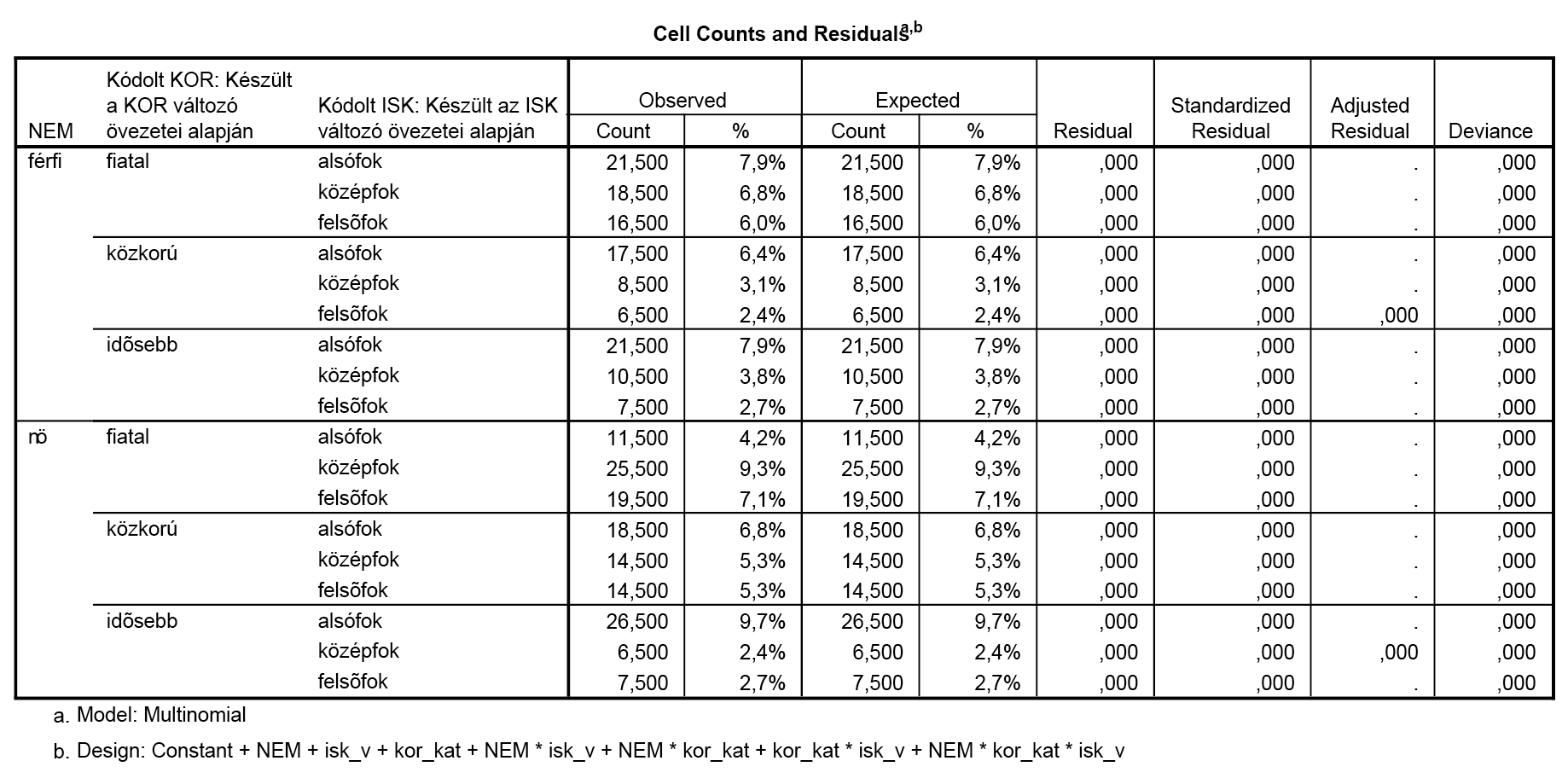
Az összes létező interakciót megadtuk – így azt várjuk a programtól, hogy teljes illeszkedést tudjunk elérni. Természetesen minden olyan esetben, amikor előre látható az eredmény, lényegében felesleges elemzést futtatnunk. Azonban más, ennél kevesebb paraméter megadásával is elérhetjük ezt a változatot, így érdemes lehet megismerni, hogy az output mely eleme tájékoztat minket arról, hogy a fenti modellben teljes az illeszkedés (lényegében nincsen benne véletlen).

A program rögtön az output elején felhívja a figyelmet a reziduálisok 0 voltára, a szignifikanciákat ilyenkor lényegében nem érdemes kiszámítani – és a táblázatból is látható, hogy minden tapasztalt és számított gyakoriság megegyezik, amiben nyilván (ahogy a leírásban is bemutattuk) semmi meglepő nem lehet, hiszen minden létező információt megadtunk a modellünkben.