A módszer technikai megvalósítását több helyen is megtalálhatjuk, de a fejezet során SPSS-ben mutatjuk be a módszer kivitelezését.

Az első példában egy olyan adatállománnyal dolgozunk, melyben az objektumok távolságai előre adottak, és e távolságok alapján szeretnénk egy olyan 2-dimenziós ábrázolást készíteni, melyben az objektumok távolságai a lehető legjobban közelítik az eredeti objektumok által definiáltakat.

A feladatot magyarországi városokkal mutatjuk be. Az objektumok közötti távolságok alapján történő ábrázolás láttathatósága nagymértékben függ az objektumok sorrendjétől, felsorolásától. Azonban mindez megfogalmazható abban a formában is, hogy az ábrázolás nem egyértelmű: különböző forgatások, eltolások, tükrözések (klasszikus értelemben vett egybevágósági transzformációk) nem befolyásolják az ábrázolás jóságát, minőségét – azonban nehezíthetik vagy könnyíthetik a végeredmény interpretálhatóságát.1

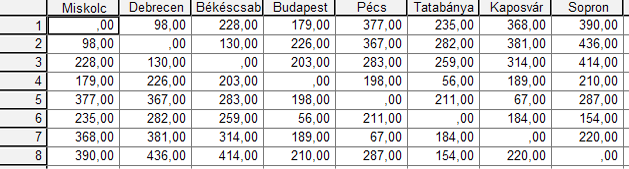
8 magyarországi várost választottunk ki, a közöttük lévő távolságot pedig az autóval megtehető legrövidebb távolságokban adtuk meg:

	Sopron	Kaposvár	Tatabánya	Pécs	Budapest	Békéscsaba	Debrecen	Miskolc
Sopron	0	220	154	287	210	414	436	390
Kaposvár	-	0	184	67	189	314	381	368
Tatabánya	-	-	0	211	56	259	282	235
Pécs	-	-	-	0	198	283	367	377
Budapest	-	-	-	-	0	203	226	179
Békéscsaba	-	-	-	-	-	0	130	228
Debrecen	-	-	-	-	-	-	0	98
Miskolc	-	-	-	-	-	-	-	0

	Sopron	Kaposvár	Tatabánya	Pécs	Budapest	Békéscsaba	Debrecen	Miskolc
Sopron	0	220	154	287	210	414	436	390
Kaposvár	-	0	184	67	189	314	381	368
Tatabánya	-	-	0	211	56	259	282	235
Pécs	-	-	-	0	198	283	367	377
Budapest	-	-	-	-	0	203	226	179
Békéscsaba	-	-	-	-	-	0	130	228
Debrecen	-	-	-	-	-	-	0	98
Miskolc	-	-	-	-	-	-	-	0

SPSS-ben az alábbi formában tároljuk ezeket az adatokat (a sorrend tehát itt most pont a fordítottja a fenti táblázatnak):

A városok közötti távolságok szimmetrikusak, de természetesen ez sem kell hogy igaz legyen – gondolhatunk itt a repülőutakra, ahol ismert tény, hogy az oda-vissza utak rendszerint nem azonosak. Hasonlóan: nem feltétlenül szimmetrikus az adatállomány akkor, ha emberek közötti szimpátiát kell pontozni, értékelni: a szimpátia ugyanis nem feltétlenül kölcsönös.

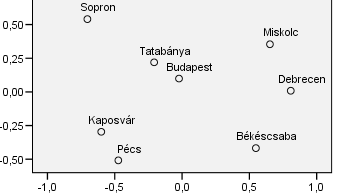
Amennyiben a fenti sorrendben szerepeltetjük a városokat, úgy az alábbi ábrázolást nyerjük:

Észrevehető, hogy az eredeti ábrázolás mértékegységei nem köszönnek vissza az ábráról (egy majdnem origó középpontú téglalap lett az ábrázolásunk alapja, melyben elhelyeztük a városokat). A városok azonban megközelítően felismerhető helyen vannak – nyilvánvalóan nem illeszthető rájuk teljes egészében egy Magyarország-térkép, de elég közelinek tekinthető a megoldás a valósághoz.

Fontos azonban kiemelni, hogy semmivel sem nyernénk jobb vagy rosszabb ábrázolást, ha a tengelyek skálázása nem −1 és 1 (illetve −0,5 és 0,5) közötti lenne, hanem pl. −10 és 10 közötti, illetve ha az egész ábrát néhány fokkal jobbra vagy balra elforgatnánk, netán az egészet az origóra tükröznénk.

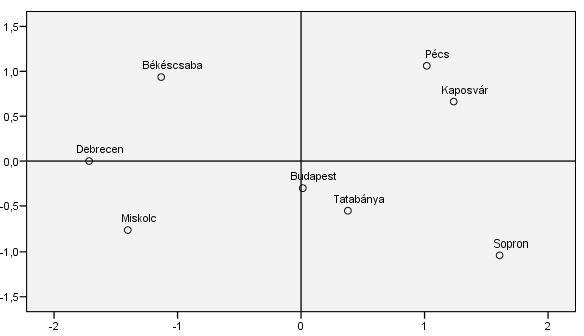
Néhány ilyen transzformációt végrehajtva például az alábbi ábrázolás nyerhető:

A városok távolságai egymáshoz képest nem változtak meg, azonban a tengelyek más skálán szerepelnek és az Észak–Dél-, illetve Kelet–Nyugat-tengelyek is megfordultak. De az ábrázolás matematikai minősége semmit sem javult vagy romlott.2

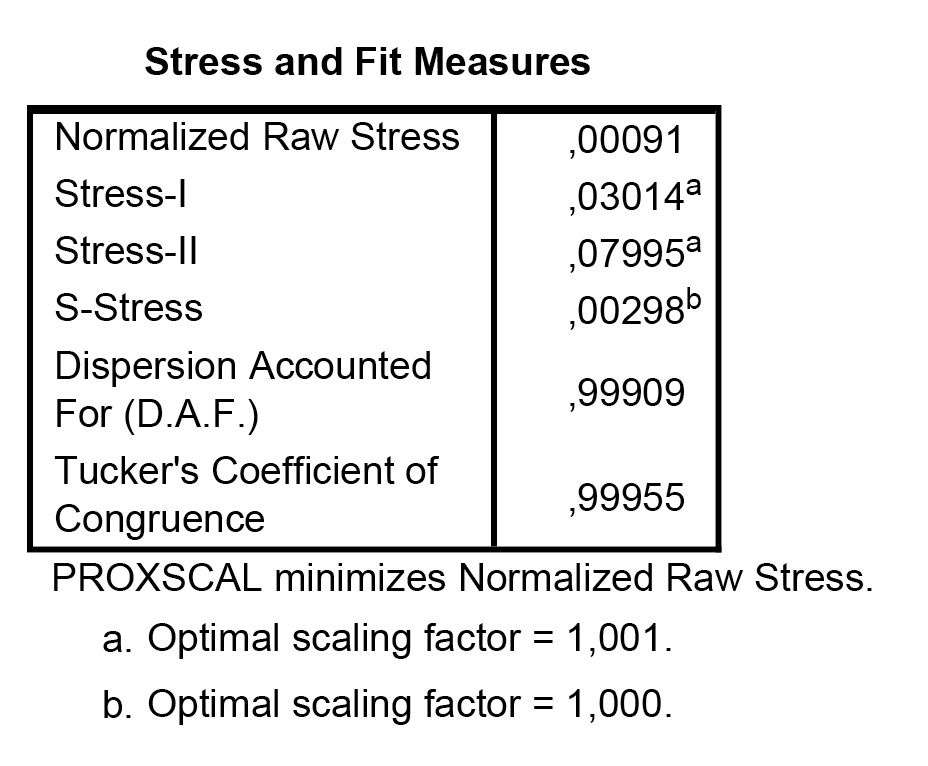
A modellek értékelése

A modelleket az s-stress mutató segítségével értékeljük tehát, mely mindegyik ábrázolás esetén 0,00298 volt, ami 0,05 alatti, tehát kiváló ábrázolást találtunk mindkét esetben – matematikailag nyilván semmi különbség nem lehetett a különböző ábrákban, ábrázolásokban.

A távolságok alapján számított ábrázolás esetén fontos lehet az objektumok felsorolásának sorrendje – és általánosságban nem számít, hogy milyen beosztású koordináta-rendszerben, vagy milyen elhelyezkedéssel ábrázolunk. Minden egybevágósági transzformáció megengedett (forgatások, eltolások), ha segítségével könnyebben interpretálható, jobban értelmezhető eredményeket nyerünk.

Jegyzetek