Az elemzés technikai megvalósítása ROPstatban

Az elemzés technikai megvalósítása ROPstatban
Azért használjuk ezen elemzésre a ROPstatot, mert egyrészt egyszerűbb az output felépítése, másrészt pedig a ROPstat rendelkezik azzal a jó tulajdonsággal, hogy a skálatípus-átállítás segítségével azonnal át tudunk lépni rangstatisztikai eljárásokra. Miután a pszichológiai változók jelentős része ordinális változó (nem normális eloszlású), így ezt az opciót mindenképpen érdemes kiaknáznunk.
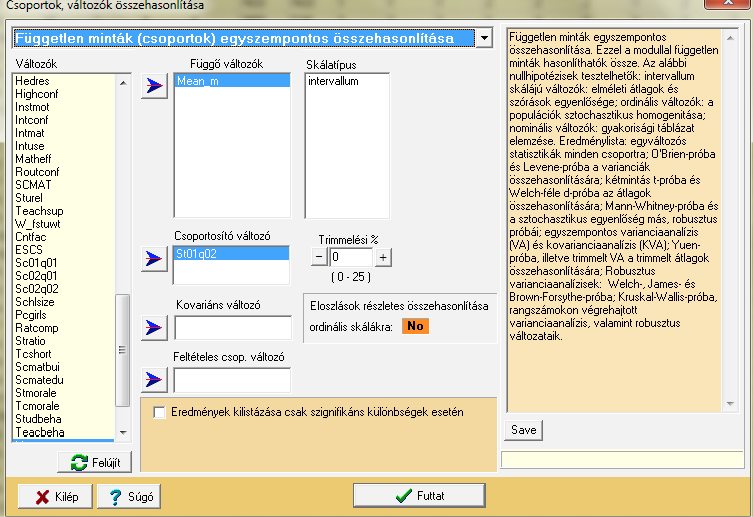
Az elemzést az egyszempontos varianciaanalízis menüpontban találhatjuk meg:
A függő változó tehát a matematika (mean_m), míg a csoportosító változó az iskolatípus (st01q02). Korábbi anyagban már ismertetésre kerültek az iskolatípusok, de álljon itt ismét:
|
Kód |
Iskolatípus |
|
1 |
Általános iskola |
|
2 |
Gimnázium |
|
3 |
Szakközépiskola |
|
4 |
Szakiskola |
Független minták egyszempontos összehasonlítása
A beolvasott összes eset száma: 1000
Csoportosító változó: St01q02 (Iskola típus (képzés típusa))
Jelölés: +: p < 0,10 *: p < 0,05 **: p < 0,01 ***: p < 0,001
FÜGGŐ VÁLTOZÓ: Mean_m (Matematika, átlag)
| Csoportonkénti alapstatisztikák | ||||||||
| Index | St01q02 | Esetek | Átlag | Szórás | Min. | Max. | Ferdeség | Csúcsosság |
| 1 | 1 | 92 | 402,14 | 67,19 | 260,43 | 599,27 | 0,239 | -0,025 |
| 2 | 2 | 335 | 558,72 | 72,38 | 365,27 | 731,22 | -0,158 | -0,351 |
| 3 | 3 | 381 | 491,21 | 68,85 | 305,37 | 742,98 | 0,170 | -0,028 |
| 4 | 4 | 192 | 407,20 | 66,77 | 216,89 | 619,29 | -0,094 | 0,105 |
Ha a Ferdeség vagy a Csúcsosság szignifikáns, az a normalitás sérülését jelzi.
Látható, hogy jelen esetben a ferdeség és a csúcsosság nem jelez sérülést, hiszen nincsenek ott a ROPstatban megszokott csillagok. Ez azt jelenti, hogy elvben nem lehet szükség a rangstatisztikai eljárásokra, hiszen innentől csak a szóráshomogenitás lesz számunkra ellenőrizendő feltétel. (Illetve, ha rangstatisztikát alkalmazunk, akkor valószínűleg nagyon hasonlatos eredményeket fogunk találni, legfeljebb ritkábban lesz szignifikáns az eltérés.)
Elméleti szórások egyenlőségének tesztelése
- O’Brien-próba (Welch-féle): F(3,0; 341,8) = 0,723 (p = 0,5391)
- Levene-próba (Welch-féle): F(3; 341,6) = 0,739 (p = 0,5296)
A szóráshomogenitási feltétel mind az O’Brien-próba (mediántól való eltéréssel tesztel), mind a Levene-próba (abszolút eltérések segítségével tesztel) szerint teljesül. Mindkét eljárás – a zárójeles megjegyezések értelmében – robusztus eljárás a csoportok szórásainak egyenlőségének tesztelésére.
Így maradhatunk a teljesen hagyományos elemzéseknél.
Elméleti átlagok egyenlőségének tesztelése
Hagyományos eljárás, amely feltételezi a szóráshomogenitást:
- Varianciaanalízis: F(3; 996) = 248,913 (p = 0,0000)***
Hatásvariancia = 1202916,3399, Hibavariancia = 4832,6828
Korrelációs hányados (nemlineáris korrelációs együttható): eta = 0,655
Megmagyarázott variancia-arány: eta-négyzet = 0,428
Itt tehát a felső blokkot kell figyelembe vennünk, hiszen teljes a szóráshomogenitás (ha sérült volna, akkor az alábbi, robusztus eljárásokat néznénk).
Megállapítható, hogy szignifikáns különbség van az átlagok között (a VA esetén p = 0,0000, azaz 5% alatti az elsőfajú hiba valószínűsége).
A megmagyarázott variancia-arány, az eta-négyzet majdnem 43%-os, azaz igazán magasnak tekinthető – a matematika-teljesítmény igen nagymértékben összefügg tehát a diákok iskolatípusával.
Robusztus eljárások, amelyeknél nem szükséges a szóráshomogenitás:
- Robusztus Welch-féle varianciaanalízis: W(3; 341,2) = 249,369 (p = 0,0000)***
- James-próba: U = 751,032 (p < 0,001)***
- Brown-Forsythe-próba: BF(3; 640) = 255,589 (p = 0,0000)***
Átlagok Tukey-Kramer-féle páronkénti összehasonlítása (k = 4, df = 996):
T12= 27,06** T13= 15,60** T14= 0,81 T23= 18,33** T24= 34,05**
T34= 19,31**
Az átlagok Tukey-Kramer-féle összehasonlítása a páros összehasonlítások azon fajtája, melyet akkor használunk, ha a szóráshomogenitás teljesül. Ezek alapján megállapítható, hogy az általános iskolások és szakiskolások teljesítménye között nincsen jelentős eltérés (T14) – míg minden más esetben szignifikáns különbségeket látunk.
Ha a szóráshomogenitás nem teljesülne, akkor az alábbi Games–Howell-tesztet kéne választani.
Ehhez az összehasonlításhoz, illetve a megfelelő összefüggések megfogalmazásához a fenti, csoportonkénti alapstatisztikákat tartalmazó fenti táblázatban lévő átlagok lehetnek a segítségünkre.
Átlagok Games-Howell-féle páronkénti összehasonlítása
(elméleti szórások különbözhetnek, zárójelben a szabadságfokok):
T12(4; 154)= 27,53** T13(4; 141)= 16,06** T14(4; 178)= 0,84 T23(4; 692)= 18,02**
T24(4; 425)= 34,37** T34(4; 394)= 19,90**
EDDIG úgy elemeztünk, hogy a szövegértés-teljesítményt NEM vettük figyelembe. A kovarianciaanalízis-blokkban már azokat az eredményeket látjuk, amikor azt feltételezzük, hogy a szövegértés-teljesítmény azonos – ekkor vannak-e különbségek az iskolatípusok között?
Kovarianciaanalízis
Kovariáns változó = Mean_r (Szövegértés, átlag)
| Index | St01q2 | n | Átlag | Korrigált átlag | r(Mean_m, Mean_r) | |
| 1 | 1 | 92 | 402,14 | 460,68 | 0,699 (p=0,000)*** | |
| 2 | 2 | 335 | 558,72 | 506,65 | 0,657 (p=0,000)*** | |
| 3 | 3 | 381 | 491,21 | 489,91 | 0,696 (p=0,000)*** | |
| 4 | 4 | 192 | 407,20 | 472,60 | 0,742 (p=0,000)*** |
Figyeljük meg a táblázatban, hogy a korrigált átlagok lényegesen kisebb sávban szóródnak, mint az eredeti átlagok – közeledtek egymáshoz a különbségek.
Mean_m és Mean_r Pearson-féle korrelációja a teljes mintán (f = 998): r = 0,827 (p = 0,000)***
Parciális korreláció a csoportosító változó kiszűrése után: r(xc.g) = 0,811 (p = 0,000)***
Elméleti csoportkorrelációk egyenlőségének tesztelése: Khi2(3) = 3,376 (p = 0,337)
Jól látható, hogy a kovariáns változó valóban összefügg a mért változóval, illetve parciálás után is jelentős összefüggés marad.
A korrigált mintaátlagokat kell tehát most összehasonlítanunk. Ez úgy keletkezik, hogy a szövegértés-teljesítményt egységes szinten tartjuk.
Korrigált mintaátlagok összehasonlítása: F(3; 995) = 16,676 (p = 0,0000)***
A korrigált mintaátlagok szintén szignifikánsan különböznek.
Korrigált átlagok Tukey-Kramer-féle páronkénti összehasonlítása (k = 4, df=995):
T12= 10,98** T13= 7,08** T14= 2,64 T23= 6,28** T24= 10,58**
T34= 5,50**
A szóráshomogenitás továbbra is fennáll (az átlagokat korrigáljuk csak, a szórások nem változnak), így megállapítható, hogy a különbségek továbbra is fennmaradnak.
Amennyiben a különbségek nem lennének szignifikánsak, úgy egy olyan jellegű kiírást látnánk, mint a Games–Howell-teszt esetén – azaz egyik páros összehasonlításnál sem látnánk *-os jelzéseket.
Korrigált átlagok Games-Howell-féle páronkénti összehasonlítása
(elméleti szórások különbözhetnek, zárójelben a szabadságfokok):
T12(4; 197)= 1,24 T13(4; 163)= 0,83 T14(4; 181)= 0,32 T23(4; 671)= 0,59
T24(4; 494)= 1,12 T34(4; 450)= 0,63