Vizsgakérdések – faktor- és főkomponens-elemzés

	I	H
A faktorelemzés egyik speciális esete a főkomponens-elemzés.	X
A főkomponens-elemzés során sok változót szeretnénk kevés változó segítségével magyarázni.	X
A faktorelemzésben mindig VARIMAX rotálást kell végezni.		X
Minél magasabb a KMO-érték, annál kevésbé összefüggőek a változóink.		X
A Bartlett-teszt segítségével arról hozhatunk döntést, hogy a változó-szettünk mennyire hasonlít egy teljesen független változó-szetthez.	X
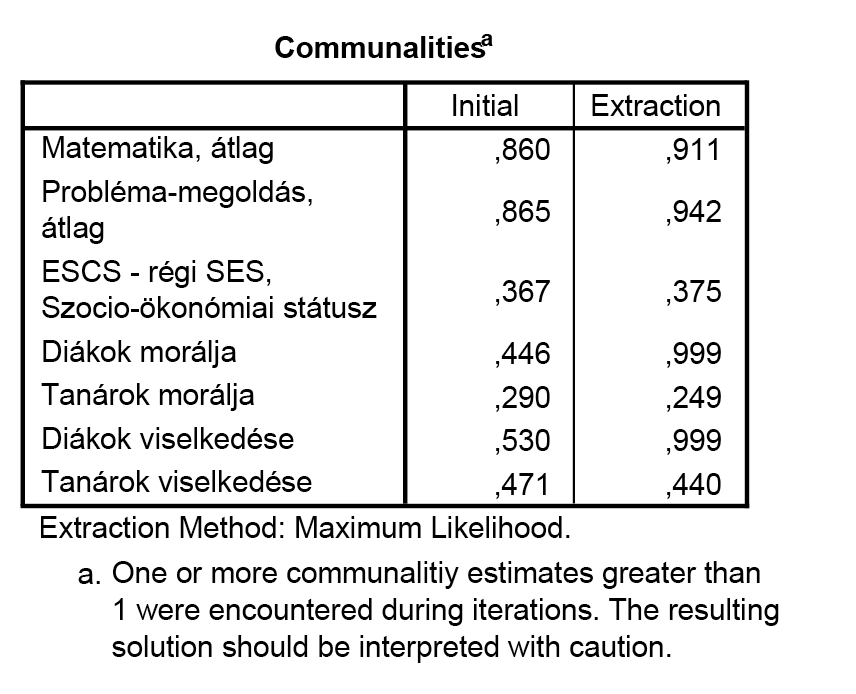
A végső kommunalitások táblázatában a jó modellek esetében általában 0,25-nél nagyobb értékeket szokás elvárni.	X
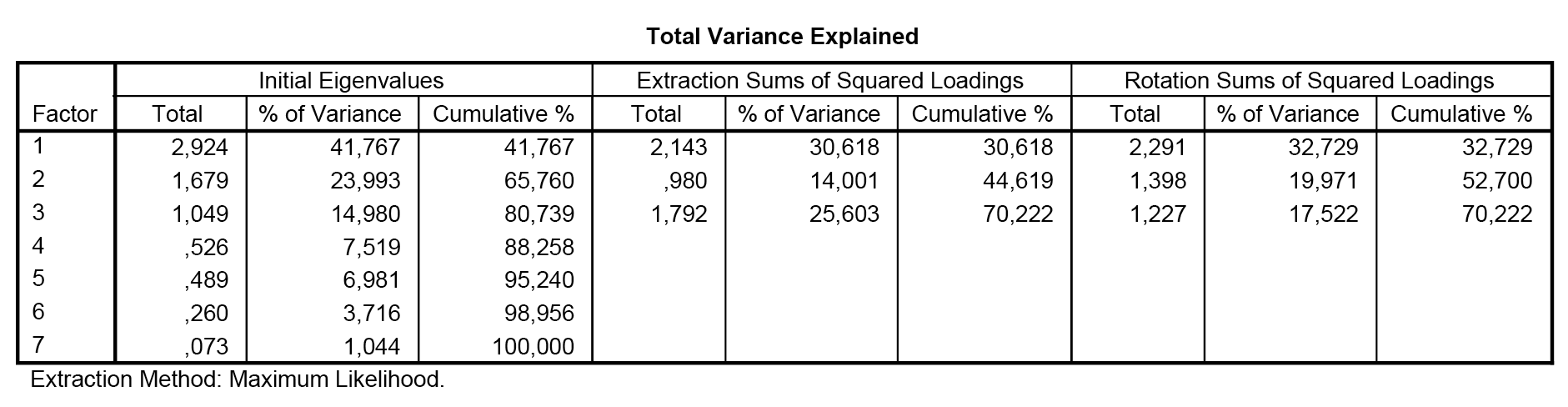
A harmadik faktor a teljes variancia 70,222%-át magyarázza.		X
Rotálás segítségével növelhető a teljes magyarázott variancia-arány.		X
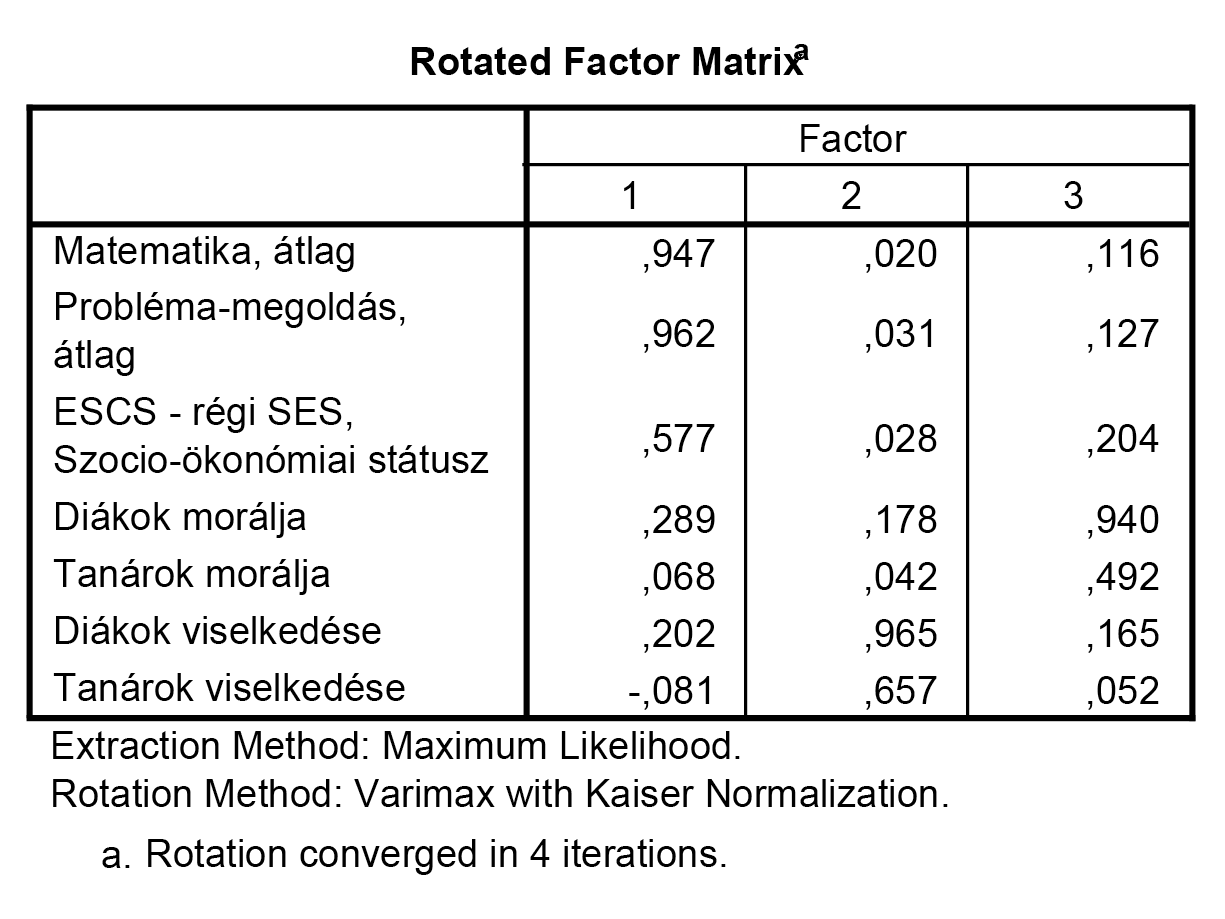
A diákok és a tanárok morálja egyértelműen a második faktorhoz tartozik.		X
A fenti modell főkomponens-elemzéssel készült.		X
A fenti eljárásban VARIMAX rotációt alkalmaztunk.	X
A diákok és a tanárok viselkedése egy faktoron helyezkedik el.	X
Rotáció után az első faktor által magyarázott variancia-arány 32,729%.	X
A KMO-érték 0,6 felett már elfogadható, így e modellünk átmegy ezen a szűrőn.	X
A tanárok morálja a 0,249-es kommunalitás alapján kihagyható lenne a modellből, így újabb futtatással kéne újabb faktorstruktúrát feltárni.	X

Hamis válaszok magyarázata

1. A faktorelemzésben mindig VARIMAX rotálást kell végezni.

2. Minél magasabb a KMO-érték, annál kevésbé összefüggőek a változóink.

3. A harmadik faktor a teljes variancia 70,222%-át magyarázza.

4. Rotálás segítségével növelhető a teljes magyarázott variancia-arány.

5. A diákok és a tanárok morálja egyértelműen a második faktorhoz tartozik.

6. A fenti modell főkomponens-elemzéssel készült.

Ha mindig VARIMAX rotálást kéne végrehajtani, akkor csak azt engedné a program. A rotálás során a magyarázhatóságot, az illeszkedést szeretnénk modellen belül javítani – ebből következően számos szempont lehet, ami alapján a rotációt végre akarjuk hajtani. Igaz ugyan, hogy a derékszögű (ortogonális) forgatások közül a VARIMAX az egyik legjobb, a ferde forgatások (melyek után a faktorok egymástól való függetlensége nem feltétel) sokat javíthatnak a modell értelmezhetőségén.
A KMO-érték magas volta azt jelzi, hogy erős összefüggések lehetnek a változók között, tehát reménykedhetünk jól magyarázható, erős háttérváltozók megtalálásában.
A három faktor együttes magyarázó ereje 70,222%, a harmadik faktor rotáció után 17,522%-ot magyaráz a teljes varianciából.
A rotálás csak átrendez, magyarázó erőt már nem rak a modellhez. Azonban kicsit kiegyensúlyozza a háttérváltozók erejét, jobban elosztja közöttük a változókat.
A diákok és tanárok morálja a harmadik faktoron van a legnagyobb súllyal, így ehhez a faktorhoz rendeljük hozzá.
A főkomponens-elemzésnél a módszernél Principal Component szerepelne – esetünkben Maximum Likelihood módszer van feltüntetve, tehát hagyományos faktorelemzést végeztünk.