Vizsgakérdések – bináris logisztikus regresszió

	I	H
A bináris logisztikus regresszióban a függő változó mindig folytonos.		X
A logisztikus regresszióban arra vagyunk kíváncsiak, hogy a függő változók adott értéke mellett mi a magyarázó változó adott értékének bekövetkezési valószínűsége.		X
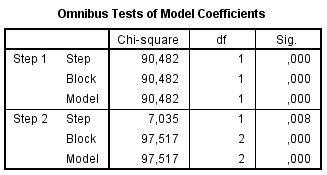
Az Omnibus-tesztek megmutatják, hogy mennyire jó illeszkedésű a modellünk.	X
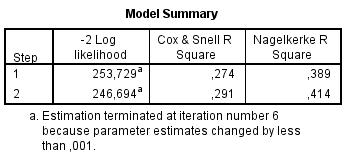
A Cox & Snell-féle mutató elvileg nem éri el az 1-et.	X
A Modell Summary táblázatban található R-négyzetek a modell determinációs együtthatói.	X
A fenti eljárásban lépésenkénti regressziót alkalmaztunk.	X
Ha a klasszifikációs táblázatok bal alsó és jobb felső sarkában vannak nagy értékek, akkor tudhatjuk, hogy jó modellt találtunk.		X
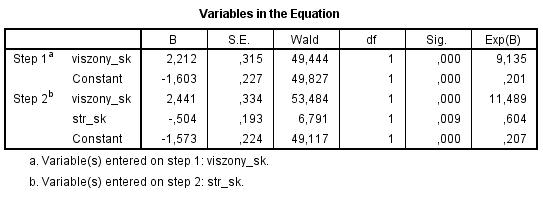
Az utolsó táblázat B oszlopában lévő negatív értékek azt jelentik, hogy a magyarázó változó növelésével csökken a diszkrét változó 1-es értékének bekövetkezési valószínűsége.	X
Az utolsó táblázat SIG-értékei azt mutatják meg, hogy az adott függő változó együtthatója 0 vagy nem 0 a modellben.		X
Az EXP(B) érték akkor negatív, ha a B érték negatív.		X
A klasszifikációs táblázatban lévő értékekből leolvashatjuk, hogy mi a tapasztalati és a modellbéli becsült eredmények egymáshoz való viszonya – hány hibás és hány helyes osztályozás történt a modell segítségével.	X
A logisztikus regresszióban feltétel a függő változó normalitása.		X
A magyarázó változók erős egymással való összefüggése rontja a modell interpretálhatóságát.	X
A Nagelkerke-féle R-négyzet elvi maximuma 1.	X
A logisztikus regresszióban a Modell Summary táblázat első oszlopában a regresszióból számított korrelációs együtthatót olvashatjuk le.		X

A hamis válaszok magyarázata:

1. A bináris logisztikus regresszióban a függő változó mindig folytonos.

2. A logisztikus regresszióban arra vagyunk kíváncsiak, hogy a függő változók adott értéke mellett mi a magyarázó változó adott értékének bekövetkezési valószínűsége.

3. Ha a klasszifikációs táblázatok bal alsó és jobb felső sarkában vannak nagy értékek, akkor tudhatjuk, hogy jó modellt találtunk.

4. Az utolsó táblázat SIG-értékei azt mutatják meg, hogy az adott függő változó együtthatója 0 vagy nem 0 a modellben.

5. Az EXP(B) érték akkor negatív, ha a B érték negatív.

6. A logisztikus regresszióban feltétel a függő változó normalitása.

7. A logisztikus regresszióban a Modell Summary táblázat első oszlopában a regresszióból számított korrelációs együtthatót olvashatjuk le.

A függő változó a logisztikus regresszióban diszkrét, bináris logisztikus regresszióban pedig bináris, azaz kétértékű, más néven dichotóm.
Fordítva: a magyarázó változók adott értéke mellett mi a függő, dichotóm változó adott értékének (1-es) bekövetkezési valószínűsége. Megjegyezzük, hogy miután csak két értéke van, ezért így a másik érték bekövetkezési valószínűségét is automatikusan tudjuk.
Ez is fordítva: a bal felső és jobb alsó sarokban láthatók a megegyező prediktív és tapasztalt egyezések, tehát a modell jóságát onnan láthatjuk, hogy e két mezőben szerepelnek magas értékek.
A magyarázó változóknak van együtthatója, hiszen a függő változóra írjuk fel a magyarázó változók segítségével az összefüggést. Azaz a SIG-értékek azt mutatják, hogy a magyarázó változóknak az együtthatója 0 vagy nem 0 a modellben.
Az EXP(B) érték egy exponenciális függvényből vett érték, ami nem lehet negatív. Ebből persze az is következik, hogy ha a B érték negatív, akkor az EXP(B) érték 0 és 1 közötti, ha a B érték 0, akkor az EXP(B) érték 1, továbbá ha a B érték pozitív, akkor az EXP(B) érték 1 feletti.
A függő változó diszkrét, bináris esetben pedig kétértékű, így a normalitás megkövetelése elég túlzó lenne…
A korrelációs együttható érték −1 és 1 közötti. Az első oszlopban látható érték pedig ezt messze meghaladja – így már az értékekből is látható, hogy semmiképpen sem lehet korrelációs együttható, amit abban az oszlopban láthatunk.