Vizsgakérdések – diszkriminancia-analízis

	I	H
A diszkriminancia-analízis (DA) során csoportokat szeparálunk egymástól.	X
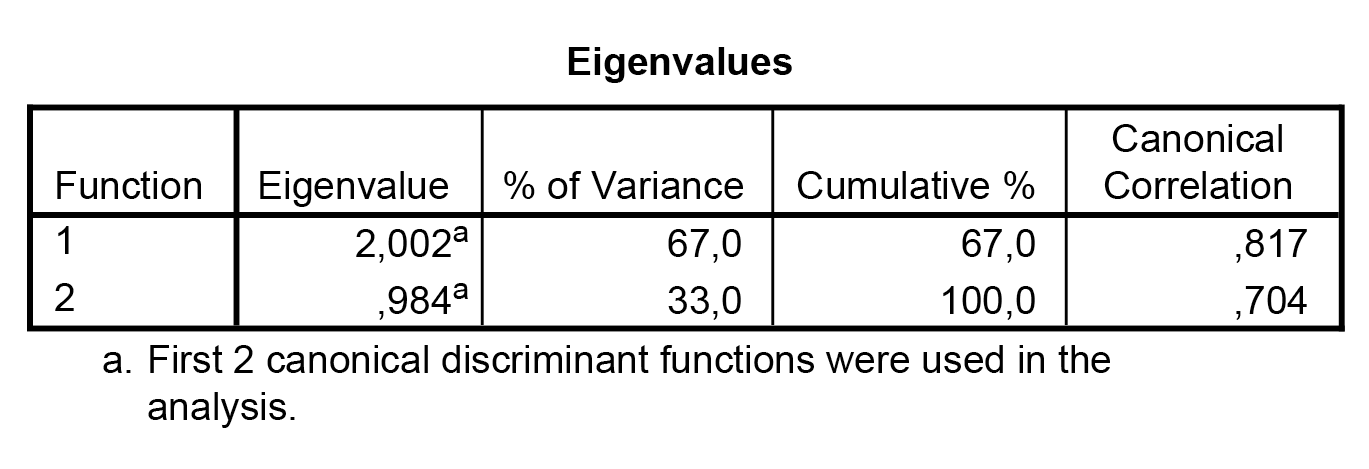
Minél nagyobb a Wilks-féle lambda értéke, annál jobb a szeparálásunk.		X
A DA során olyan függvényeket határozunk meg, melyek egyben tartják a populációt.		X
A DA során azok a függvények, melyek szeparálnak, mindig lineárisak.	X
Az 1-es csoport az első függvényen átlagosan negatív, míg a másodikon átlagosan pozitív értékekkel képviselteti magát.	X
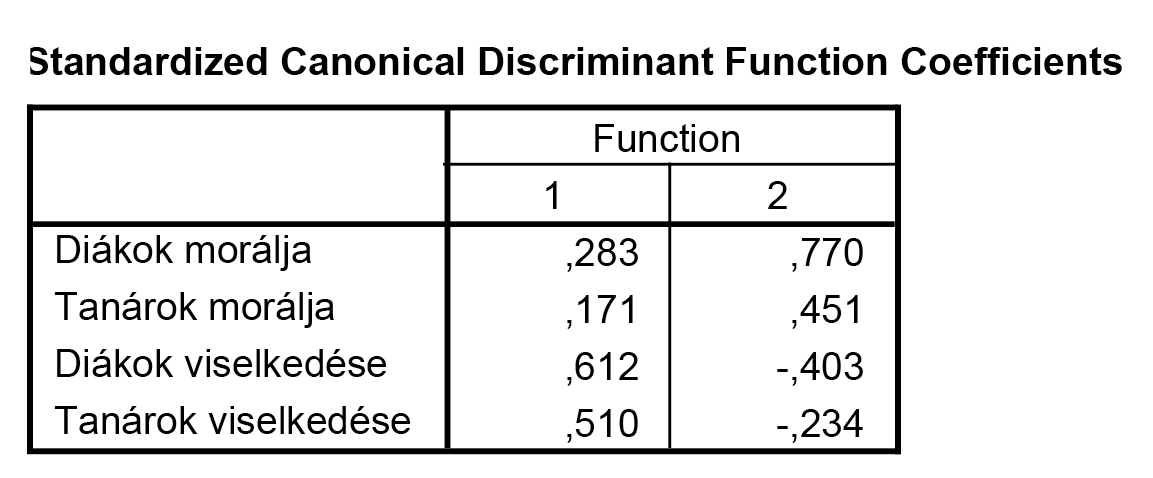
A második függvényben a viselkedés-változók pozitív, míg a morál-változók negatív együtthatóval vesznek részt.		X
A Wilks-féle lambda-érték egy fordított determinációs együtthatóként értelmezhető.	X
A 3 csoportot 2 függvény segítségével tudjuk egymástól elkülöníteni.	X
Amennyiben „n” darab csoportunk van, úgy „n” függvény mindenképpen elegendő a szétvágásukhoz.		X
A logisztikus regresszió során is diszkrét változókat azonosítunk, de amíg ott a bekövetkezések valószínűsége a kérdés, addig itt a csoportok szeparálása, elkülönítése.	X
A DA során a függő változó mindenképpen folytonos.		X
A sajátértékek segítéségével megállapítható, hogy melyik függvénynek van nagyobb szeparáló ereje, képessége.	X
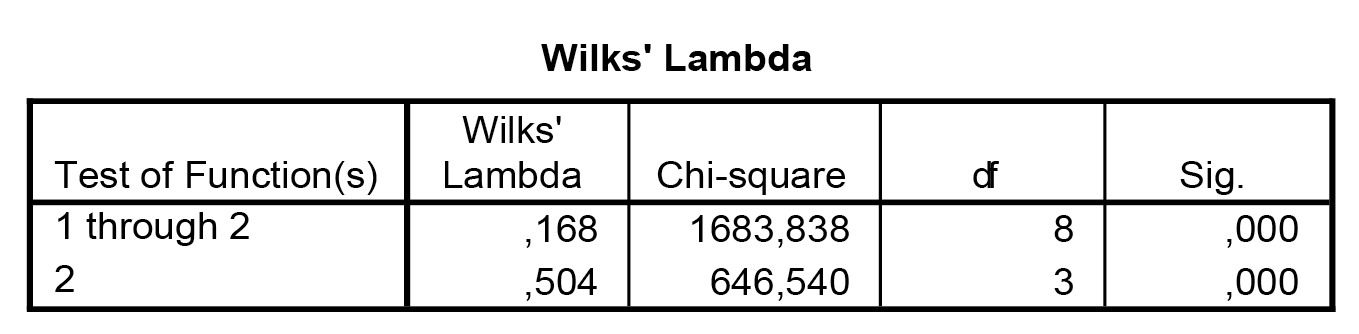
A Wilks-féle lambda SIG-értéke mutatja meg, hogy mely változó segítségével lehet a csoportokat szignifikánsan elkülöníteni.		X
A DA csak bináris változókra alkalmazható.		X
A fent ismertetett eljárásban a k-középpontú klaszterezés egyfajta ellenőrzésére használtuk a DA-t.	X

A hamis válaszok magyarázata:

1. Minél nagyobb a Wilks-féle lambda értéke, annál jobb a szeparálásunk.A Wilk’s lambda értéke minél nagyobb, annál jobb a szeparálásunk.

2. A DA során olyan függvényeket határozunk meg, melyek egyben tartják a populációt.

3. A második függvényben a viselkedés-változók pozitív, míg a morál-változók negatív együtthatóval vesznek részt.A második függvényben a „viselkedés” változók pozitív, míg a „morál” változók negatív együtthatóval vesznek részt.

4. Amennyiben „n” darab csoportunk van, úgy „n” függvény mindenképpen elegendő a szétvágásukhoz.Amennyiben van „n” darab csoportunk, úgy mindenképpen „n” függvény elegendő a szétvágásukhoz.

5. A DA során a függő változó mindenképpen folytonos.

6. A Wilks-féle lambda SIG-értéke mutatja meg, hogy mely változó segítségével lehet a csoportokat szignifikánsan elkülöníteni.A Wilk’s lambda SIG értéke mutatja meg, hogy mely változó segítségével lehet a csoportokat szignifikánsan elkülöníteni.

7. A DA csak bináris változókra alkalmazható.

Fordítva: minél kisebb, annál jobb a szeparálás.
A DA során szeparálni szeretnénk, tehát az állítással éppen ellenkezőleg,minél inkább szeretnénk olyan vágásokat, hasításokat találni, melyek jól elkülönítik egymástól az egyedeinket, csoportjainkat.
A második függvényben a „viselkedés”-hez tartozó két változó negatív, míg a „morál”-hoz tartozó változók pozitív együtthatóval vannak a táblázatban megjelölve.
N darab értéket N–1 vágással tudunk elválasztani. (Ha két értékünk van, akkor őket 1 vágással választhatjuk el, ha 3 csoport van, akkor 2 vágás elegendő, és így tovább).
A DA során a függő változó diszkrét (folytonos változónál végtelen sok vágás kellene), illetve folytonos változónál magát a változót szeretnék meghatározni, közelíteni, így az valójában egy regressziós feladat lenne.
A Wilk-féle lambdához tartozó SIG-érték annyit mutat számunkra, hogy sikerült-e szignifikáns mennyiségű szeparáló erőt meghatározni, sikerült-e érdemi vágásokat létrehozni a csoportok között.
A fenti példa is egy 3 értékű változóra alkalmazott DA-t mutat be, tehát nem csak kétértékű, azaz bináris változóra alkalmazható ez az eljárás.