Második példánkban változókat szeretnénk elhelyezni egy 2-dimenziós ábrán – így keresve kapcsolatokat, összefüggéseket. Az ábrázoláshoz egy politikai felmérés adatait használjuk, melyben parlamenti pártokról különböző, a választók számára fontos értékeket kellett pontozni.1 Az alacsony pontszámok azt jelentették, hogy az adott párt nem jellemezhető az adott értékrend hatékony képviseletével – míg a magas értékek azt jelentették, hogy kellő képviseletet, hangsúlyt kap az adott értékrend a párt célkitűzéseiben.

Ezen túlmenően a megkérdezettek azt is elmondták, hogy számukra mennyire fontos az adott értékrend a személyes életükben, életvitelükben.

4 kiválasztott értéket fogunk vizsgálni:

• szabadság,
• hagyományőrzés,
• hit,
• türelem.

4 parlamenti pártra vonatkoztatjuk a kérdéseket (azaz: a megkérdezett szerint az adott párt számára mennyire fontos az adott értékrend képviselete). A 4 parlamenti párt a FIDESZ, az MSZP, az LMP és a Jobbik. Az ábra átláthatósága miatt minden esetben az alábbi kódokat használtuk:

Elnevezés	Rövidítés
Megkérdezett	Ő
FIDESZ	F
MSZP	M
Jobbik	J
LMP	L
szabadság	szab
hagyományőrzés	hagy
hit	hit
türelem	tür

Ezek után például a megkérdezett számára mennyire fontos a hagyományőrzés az „Ő_hagy” felirattal szerepel, míg például az a változó, mely azt méri, hogy az LMP számára mennyire fontos a megkérdezett megítélése szerint a szabadság, az „L_szab” címkével jelenik meg az ábrán.

Itt némiképpen máshogy kell eljárni a programban, de továbbra sem túlságosan bonyolult a változók elhelyezése – arra kell figyelni, hogy most nem előre megadott távolságok vannak, hanem a programnak magának kell a számításokat elvégeznie.

1. ábra: a parlamenti pártok politikai térképe

A jobb felső kvadránsban helyezkednek el a megkérdezettek és az általuk véleményezett értékek. Ennek alapján elmondható, hogy a felsorolt értékek közel azonos mértékben voltak fontosak a megkérdezettek számára – továbbá az is elmondható, hogy megítélésük szerint az MSZP és a FIDESZ értékei mind egymástól, mind a megkérdezettek értékeitől közel azonos mértékben voltak távol. Ugyanakkor az LMP és a Jobbik által képviselt értékek távolra kerültek a megkérdezettektől.

Jól kirajzolódik a térkép alapján az is, hogy a 4 parlamenti párt értékei egymástól igen távolinak mondhatók – és hogy mindez a két kisebb párt esetén fokozottan távoli a választók értékeitől.

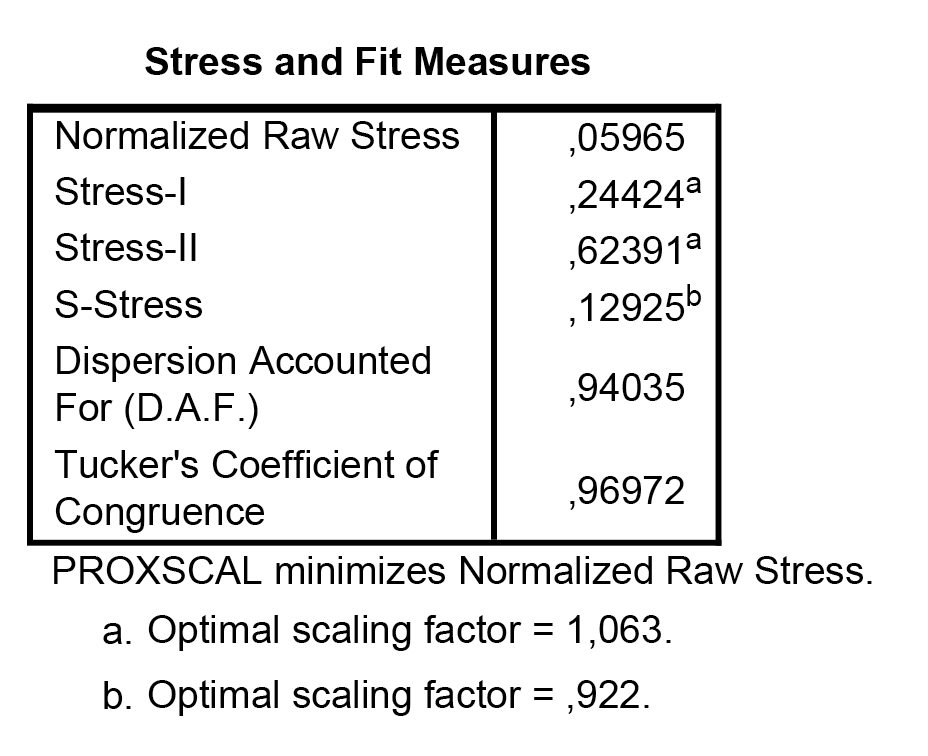
A modell értékelése

Az s-stress mutató értéke 0,13 volt, tehát nem 0,05 alatti, de még az elfogadható határon belül maradtunk a megadott táblázat tanúsága szerint. Világos, hogy itt a távolságok nem annyira egzakt módon megfogható fogalmak, mint az első esetben: egy-egy változópár távolságát az definiálja, hogy az egyes megkérdezettek szerint milyen mértékben köthető egy-egy párthoz egy-egy érték. Az így kialakuló skálán való értékelésbeli különbségek adják a hasonlóságokat/különbségeket az egyes pártok egyes értékei kapcsán.

A változók szempontjából tehát irreleváns a tájolás – hiszen nincsen jelentősége északnak vagy délnek, ellentétben például a térképek ábrázolásával. Számít viszont az objektumok/változók egymástól való távolsága, egymáshoz való viszonya. Ennek segítségével dönthetünk például arról, hogy egyes kérdések egy-egy indexben, skálában összevonhatók-e (bár ezek csak kiindulópontjai lehetnek skálák megalkotásának). Ugyanakkor ne feledjük el ilyen esetben azt sem, hogy egyes, egymástól távol kerülő változók2 esetén könnyen elképzelhető, hogy azonos jelenséget mérnek, csak a kérdések fordított tételeket tartalmaznak, és így egymástól „távolra” kerültek.

E most leírt módszerhez nem adunk meg próba-vizsgakérdéseket, hiszen ez nem képezi a képzés anyagát – azonban e melléklet segítségével alapelemzések végrehajtására képesek lehetünk, illetve az első, induló lépéseket mindenképpen megtehetjük.

Jegyzetek