Lefuttatva az elemzést az alábbi outputok fontosak számunkra:

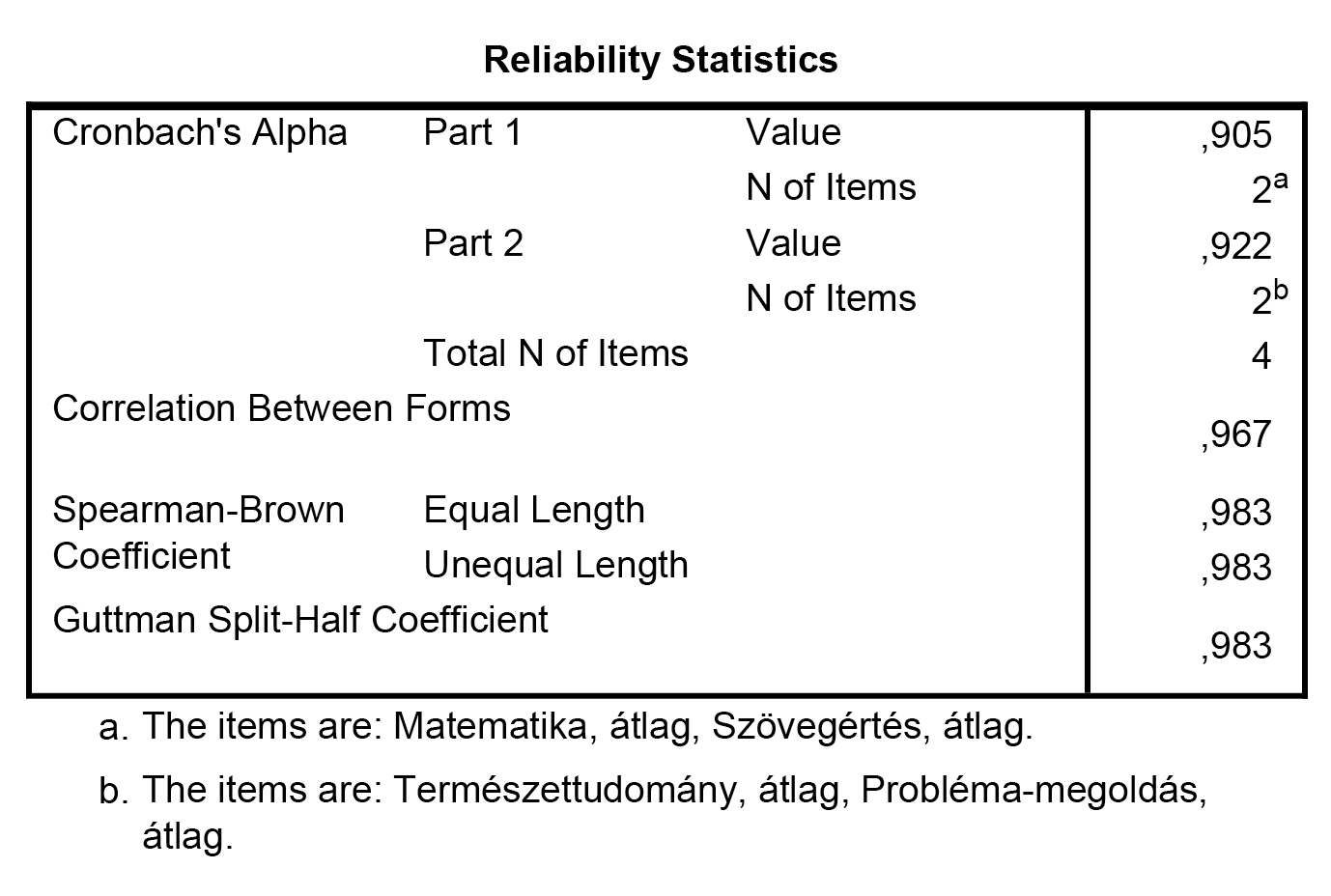
Először a Cronbach-alfa értékét fogjuk megfigyelni. Ha a fentiek szerint két részre szedjük az itemeket, 0,9 feletti eredményeket érünk el külön-külön két skálát értelmezve, mely két rész között 0,967-es Cronbach-alfa-mutatót mér a program.

Ennek értelmében az egyesített – vagy szétbontás utáni újraegyesített – skála Cronbach-alfa értéke a Spearman–Brown-együttható, melyek közül most mindkettő 0,983-as értéket mutat. (Megjegyezzük, hogy ezek után érdemes mindig futtatni egy Alpha metódus szerinti elemzést is, mert a split-half módszerrel számított alfa-érték függ attól, hogy miként osztottuk szét az itemeket két skálára. Többek között úgy is interpretálható az alfa-érték, mint az összes lehetséges módon split-half módszerrel kiszámított alfa-értékek átlaga.)

A Cronbach-alfa-értékeknek nem kell külön táblázatot készítenünk, hiszen általánosságban elmondható, hogy értékelésekor lényegében a korrelációs együtthatókra vonatkozó általános értékelések jöhetnek szóba (A 0 körüli értékek gyenge konzisztenciát takarnak, míg a 0,9 vagy afeletti értékek már-már gyanús redundanciát mutathatnak – azaz az itemek valószínűleg majdnem ugyanazt mérik). Általánosságban a 0,7–0,8 közötti értékek elfogadhatók.

A korrelációs együtthatók negatívak is lehetnek, azonban ha a Cronbach-alfa negatív értéket vesz fel, akkor gyanakodhatunk, hogy fordított item került az elemzésünkbe (a ROPstat ezt automatikusan kezelni tudja, míg az SPSS-ben ilyenkor a megfelelő itemet újra kell kódolnunk, meg kell fordítanunk „helyes”, megfelelő irányba a kódolásunkat).

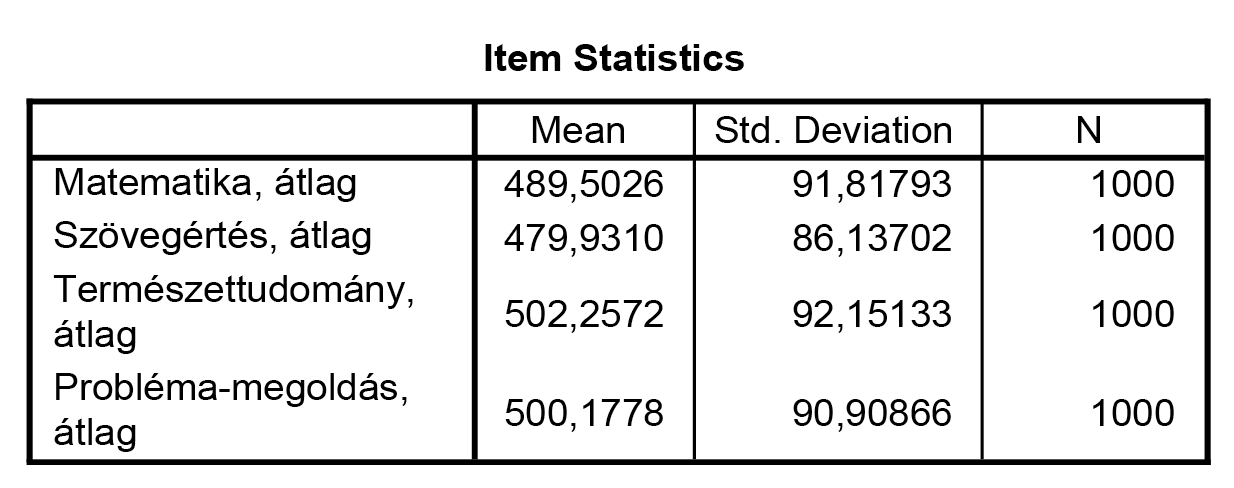
Az itemek leíró statisztikai jellemzőit általában ekkorra már kívülről tudhatjuk (egy elemzés során nem a Cronbach-alfa-elemzések az elsők, amiket elvégzünk).

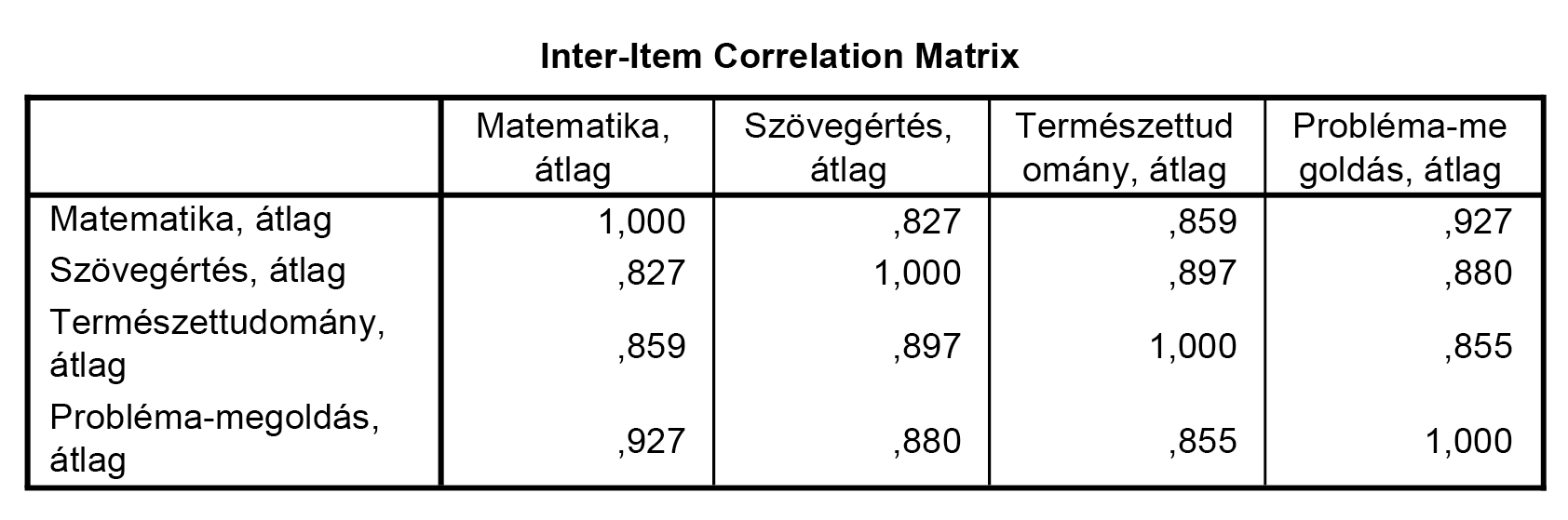
Általában az is igaz, hogy a Cronbach-alfa kiszámítása előtt már elvégeztük azokat az elemzéseket, melyek során az itemek egymáshoz való viszonyát feltártuk – így a közöttük lévő korrelációs, sőt akár különböző parciális korrelációs együtthatók is mind ismertek már. Azonban döntésünk meghozatalakor kényelmi okokból jobb, ha ezek az értékek is rögtön kéznél vannak. Így nem kell újabb és újabb output-ablakokat nyitogatnunk ahhoz, hogy az esetleges anomáliákat vagy problémás itemeket megtaláljuk.

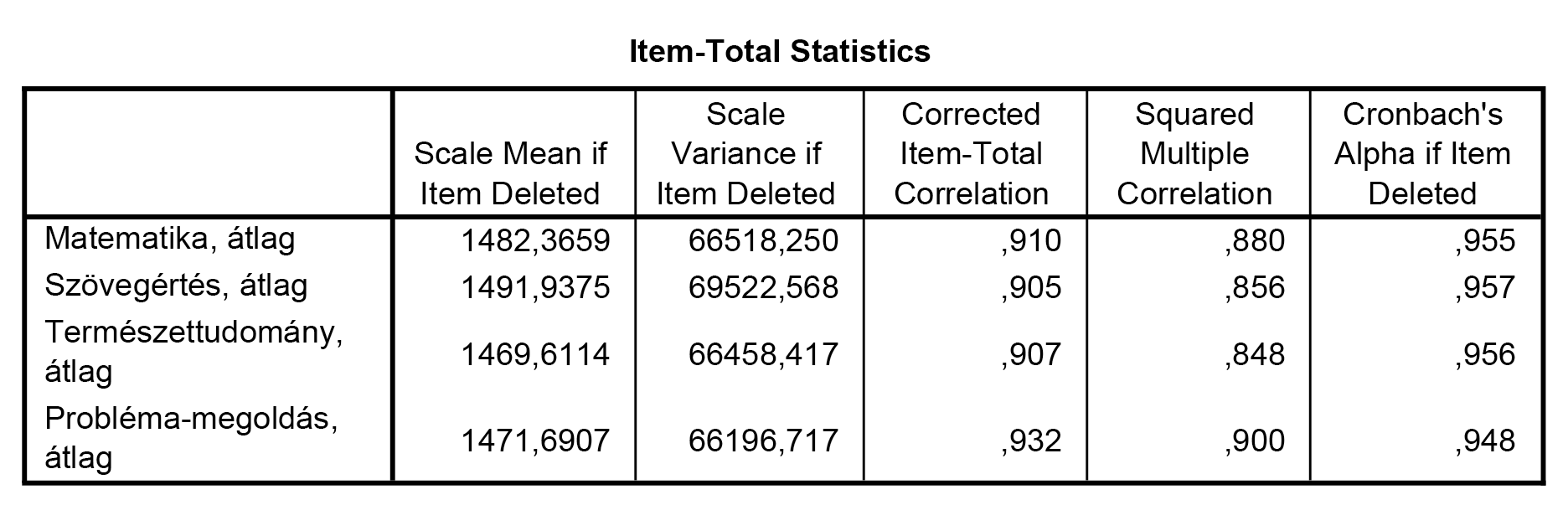
Az itemek leíró statisztikáiból ez a táblázat a leginkább hasznos számunkra, hiszen ennek utolsó oszlopa tartalmazza azt az információt, hogy mekkora lenne a Cronbach-alfa értéke, ha az egyes itemeket eltávolítanánk a skálából. Azaz ha érdemi növekedést tapasztalunk a Cronbach-alfa értékében, akkor egy-egy itemet törlünk, majd ezen item nélkül futtatjuk újra az elemzést. A megmaradó itemekkel értékeljük ki újra a kapott értékeket – mindezt addig folytatva, amíg már nem tapasztalunk érdemi növekedést (vagy az itemek száma nem redukálódik kettőre, hiszen abból már nem nagyon tudunk több itemet elvenni úgy, hogy még skálánk is maradjon).

Jól látható, hogy esetünkben bármely item elhagyása esetén is kellően magas alfa-értékekkel bírunk (ezt a split-half metódus is megerősítette, hiszen még 2-2 item összevonásával is 0,9 feletti értéket mérünk).

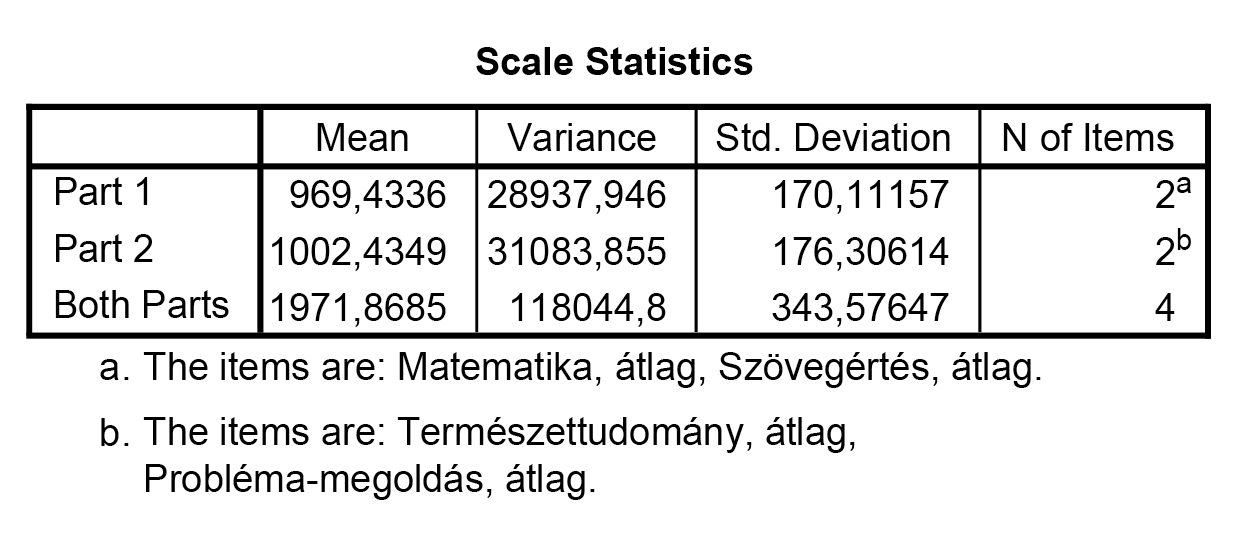
Amennyiben skálákat alkotnánk, úgy a fenti leíró statisztikai jellemzőkkel bírna a rendszer által kiválasztott két skála. Ha ehelyett a két változó/item átlagát tekintenénk, úgy ezen értékek módosulnának.

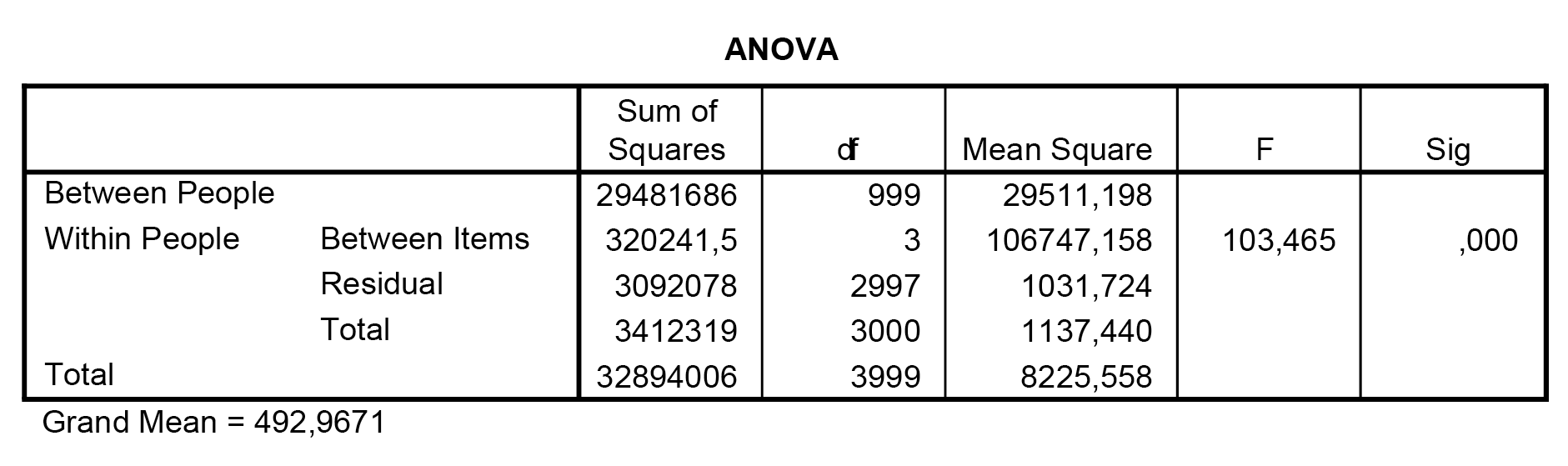
Az ANOVA táblázat adatai az mutatják meg, hogy az egyes emberek között (between) vagy egy-egy ember esetében az itemek között (within) tapasztalható-e nagyobb variabilitás. Megfigyelhető, hogy az emberek közötti különbségek lényegesen nagyobbak, mint az 1-1 itemen mért eltérés – így megállapítható, hogy egy igen erős konzisztenciával bíró átlagot tudnánk e 4 teljesítmény-változó segítségével készíteni. Ennek másfajta megfogalmazása: vélelmezhetően igen hasonló készségeket, képességeket, hátteret mérnek ezek a változók – legyenek bár igen hangzatosan, különböző nevekkel illetve.