A viszony-változó pozitív paramétere azt mutatja, hogy a változó növekedésével az együttműködés valószínűségének növekedése jár együtt (amennyiben a stresszhelyzet változatlan), míg a stressz-változó negatív volta azt mutatja, hogy ha a viszony-változó nem változik, úgy a stresszhelyzet csökkenése szintén az együttműködés valószínűségét növeli.

Azaz az erős együttműködés valószínűsége különböző viszony- és stressz-értékek alapján a fenti formulával adható meg. Például egy EXCEL-táblázat segítségével e fenti formula könnyen kiszámolható és alkalmazható. Használatának lépései a következők:

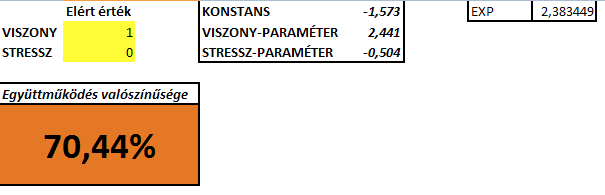
Azaz a fenti esetben egy átlagos viszony-mutató (0 – mely a standardizálás miatt az átlagos értéket jelenti) és átlagos stresszhelyzet mellett (szintén 0) elmondható, hogy nagyjából 17% annak a valószínűsége, hogy a versengő felek között erős együttműködés alakuljon ki. Azonban, ha azt gondoljuk (mérjük), hogy a versengő felek jó viszonyban vannak egymással (átlagtól 1 szórásnyira, tehát kifejezetten jó a viszonyuk), a verseny pedig átlagos stresszel jár, akkor annak a valószínűsége, hogy erős együttműködést fogunk tapasztalni, már lényegesen nagyobb, 70%-os lesz.

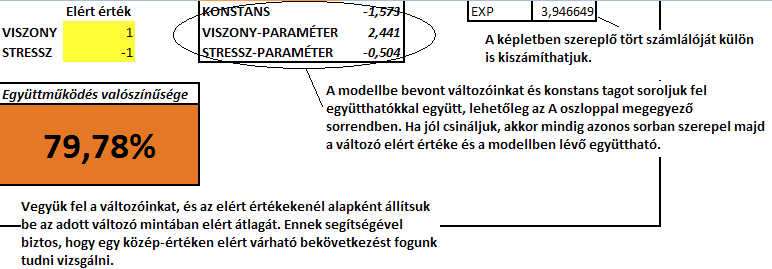
Újabb változtatás mellett az előzőekhez képest a viszony értéke továbbra is jó, míg a versenyhelyzetről azt gondoljuk, hogy az átlagosnál lényegesen kevesebb stresszel jár. Ekkor az előző 70%-hoz képest már majdnem 80%-os a valószínűsége annak, hogy erős együttműködést tapasztaljunk.

Módosítások átvezetése – újabb elemzési adatok használata

Amennyiben a modellünk változik, a következő EXCEL-béli módosításokat kell végrehajtani, hogy továbbra is hasonló becsléshez juthassunk.

Egy mintafájl és egy EXCEL-táblázat segítségével – a PDF mellett – kipróbálhatjuk e fenti elemzés elvégzését, reprodukcióját.

Mindez azt is jelenti, hogy ha saját magunknak készítünk ilyen elemzést, akkor első, alap helyzetben a vizsgált, illetve modellben szereplő változók átlagainak beírásával érdemes kezdeni a valószínűség meghatározását – majd utána természetesen a változó leíró statisztikáinak segítségével például egy szórásnyi távolságokban is vizsgálódhatunk, hogy a függő változó két lehetséges értéke milyen valószínűséggel vétetik fel a magyarázó változóink különböző értékei mellett.