3.1. Egy változó nagyságszintjének tesztelése

3.1. Egy változó nagyságszintjének tesztelése
Mostantól minden esetben megfogalmazzuk – a példáknál is látott – szakmai jellegű hipotéziseket, illetve felírjuk azt is, hogy mindez a statisztikai megfogalmazásban hogyan fest. Így könnyű ugyanis lefordítani a magunk számára a programok outputját, továbbá megkönnyítjük magunk számára a statisztikai eredmények szakmai nyelvre történő lefordítását.
- Igaz-e, hogy a vizsgált populációban az IQ-változó átlaga 100?
A fenti megfogalmazás szakmai hipotézisként is felfogható – bár szakmai hipotézisnek megfelelne pl. az is, hogy „Igaz-e, hogy a vizsgált populáció átlaga nagyobb / kisebb, mint 100?”.
A statisztikai hipotézis azonban – a korábbi megjegyzés miatt – mindenképpen ez lesz:
„Igaz-e, hogy a vizsgált populációban az IQ-változó átlaga 100?”, hiszen statisztikailag mindig egyenlőséget tudunk tesztelni.
A fenti feladat esetén lép előtérbe az, hogy a vizsgált változónkra alkalmazható statisztikai módszerek milyen feltételekkel alkalmazhatók. Tekintsük át a módszereket a feltételeikkel együtt – hogy megfelelő módszert tudjunk választani e kérdés eldöntésére:
Hagyományos esetben a fenti kérdés eldöntésére t-próbát alkalmazunk, melynek használatához szükséges a változó normalitása (nagy minták esetén ettől eltekinthetünk).
Amennyiben a normalitás sérül, úgy két lehetőségünk van:
- Robusztus t-próbát használunk (Johnson és Gayen), melyek a változó ferdeség és / vagy csúcsosság paraméterével kontrollálják a t-próba statisztikáját, elérve így, hogy az átlagra egy robusztus (adott szignifikancia-szintet tartó) eljárást nyerjünk.
- Nem az átlagot teszteljük, hanem a mediánt. Ennek feltétele a változó szimmetrikussága (tehát, ha a ferdeség szignifikánsan eltér 0-tól, akkor ez továbbra sem járható út), így amikor ez sérül, az előjelpróba alkalmazható, melynek egyetlen feltétele a változó ordinális skálázása (nyilván egy nominális változó esetén sok értelme nincsen középértékét tesztelni).
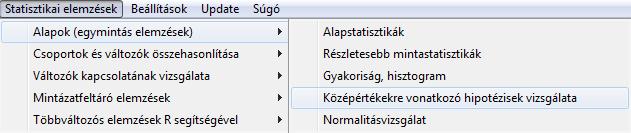
Ezen próbák közül az SPSS alapvetően az első verzióra alkalmas (ez persze nyilván túlzás, de azt fogjuk csak megnézni), míg a ROPstat egy menüpontban az összes verziót kiszámítja számunkra, így ezen hipotézisek eldöntésére alapvetően a ROPstat programcsomagot javasoljuk.
Egy változó nagyságszintjének tesztelése – ROPstat programcsomagban
Amennyiben mindenben helyesen jártunk el, az alábbi outputot kapjuk:
A beolvasott összes eset száma: 94
Jelölés: +: p < 0,10 *: p < 0,05 **: p < 0,01 ***: p < 0,001
VÁLTOZÓ: IQ (IQ of subjects)
Érvényes értékek száma: 94
Átlag: 133,70
Szórás: 13,85
Medián: 135
Minimum: 90
Maximum: 160
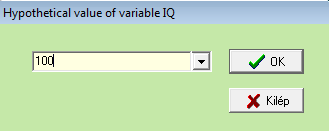
Hipotetikus érték: 100
A normalitás tesztelése a Ferdeség és a Csúcsosság segítségével:
Ferdeség: -0,572 (p = 0,024)*
Csúcsosság (g4 = a4 - 3): 0,421 (p = 0,405)
A H0: Az elméleti átlag = 100 nullhipotézis vizsgálata:
- Egymintás t-próba: t(93) = 23,588 (p = 0,0000)***
A H0: Az elméleti medián = 100 nullhipotézis vizsgálata:
- Wilcoxon-próba: R- = 5,5, R+ = 4459,5, z = 8,403 (p = 0,0000)***
A H0: P(X < 100) = P(X > 100) nullhipotézis vizsgálata:
- Előjelpróba: #(X < 100) = 2 (2,1%), #(X > 100) = 92 (97,9%), z = 9,180 (p = 0,0000)***
Az output struktúrája: először az eljárást olvashatjuk le, majd a teljes esetszámot. Utána egy jelölésrendszer következik, hogy a különböző statisztikák melletti * vagy + jel milyen szignifikancia-szintet jelöl (mekkora az elkövethető elsőfajú statisztikai hiba valószínűsége).
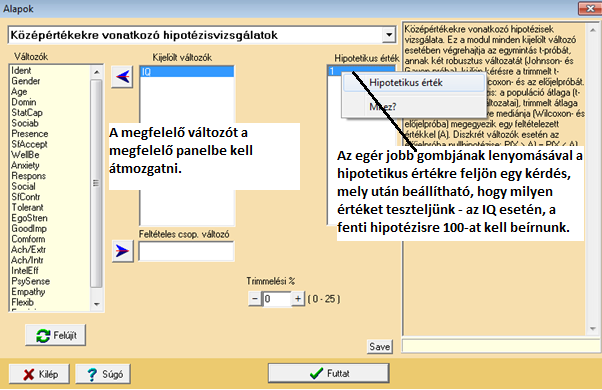
A jelölések után a változó leíró statisztikai jellemzői következnek táblázatos formában, illetve annak alján a tesztelendő hipotetikus értéket is kiírja a program, hiszen elviekben egyszerre több változót is vizsgálhatnánk, más és más hipotetikus értékekkel.
A leíró statisztikák után a normalitás tesztelése következik, ahol jól láthatóan a ferdeség sérülése némi bizonytalanságot okozhat, hogy a t-próba alkalmazása megfelelő-e a 100-as átlag tesztelésére (ezt majd feloldjuk).
Ezek után 3 tesztelés következik: az első a hagyományos, egymintás t-próba, ahol a t(93) = 23,588 (p = 0,0000)*** jelenti azt, hogy a t-statisztika 93-as szabadsági fokon számított értéke 23,588, melyhez tartozó elsőfajú hiba valószínűsége igen csekély (0,0000), az átlag egyébként 133,7.
A másik teszt a Wilcoxon-statisztika, melyben a mediánt teszteljük, illetve azt, hogy a változó mediánja lehet-e 100 – itt a z = 8,403, illetve p = 0,0000 mutatja azt, hogy a medián is igen távol van hipotetikus 100-as értéktől (medián = 135).
Az utolsó próba az előjelpróba, melynek során azt vizsgáljuk, hogy 100-as érték alatt, illetve 100-as érték felett azonos valószínűséggel kapunk-e értéket? Az ehhez tartozó z-érték 9,18, p-érték pedig 0,0000, azaz itt is világos, hogy 100 alatt és felett nem ugyanolyan valószínűséggel tartózkodunk, sőt. Azt is leolvashatjuk, hogy 100 alatt kisebb valószínűséggel (2,1%) vagyunk, mint felette (97,9%).
Az átlag tesztelésekor akkor lett volna indokolt a robusztus, átlagtesztelő eljárások bevetése, ha az elemszám 500 alatti (ez most teljesül, hiszen 94 fős a minta), és a t-érték nem túl nagy (abszolút értéke nem haladja meg a 10-et). Azonban most olyan nagy volt a t-érték, hogy a két robusztus teszt sem hozott volna érdemileg több információt számunkra, mint a t-próba (olyan nagy a különbség a hipotetikus és a számított érték között, hogy a tévedés valószínűsége elenyészően kicsi).
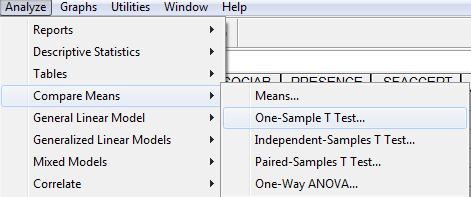
Egy változó nagyságszintjének tesztelése – SPSS programcsomagban
Az SPSS-ben tehát hagyományos egymintás t-próbát használhatunk, ahol nem lesz beépített normalitás-tesztelés, tehát itt mindenképpen meg kell előznie az előző fejezet végén használt normalitás-vizsgálatnak egy ilyen típusú elemzést!
Amennyiben megfelelően jártunk el, az alábbi outputot nyerjük:
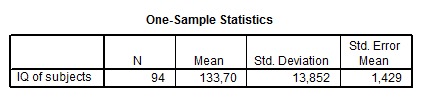
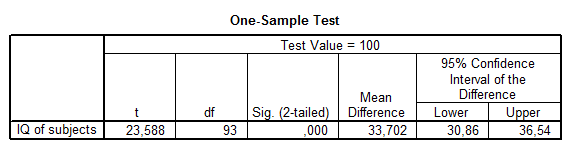
Az első táblázatban itt is a leíró statisztikákat láthatjuk, míg utána magát a t-próbát. A táblázat oszlopai sorrendben tartalmazzák a ROPstattal megegyező információtartalmú adatokat. Először a vizsgált változó nevét (felső sorban a tesztelendő értékkel), míg utána a t-értéket, szabadsági fokot (df) és a szignifikancia-szintet. Ezen kívül az átlag különbségét, illetve az átlag 95%-os konfidencia-intervallumát.
Megjegyezzük, hogy ebből az intervallumból származó értékek azok, melyektől nem különbözik szignifikánsan a számított átlag, azaz: ha innen származna a hipotetikus érték, akkor nem tapasztalnánk szignifikáns különbséget.
Műhelymunkabeli megfogalmazás
Az „IQ-változó átlaga = 100” hipotézis tesztelése
A mintába került 94 fő adatai alapján azt állíthatjuk, hogy a vizsgált populáció 133,7-es IQ-átlaga szignifikánsan magasabb, mint 100 (t = 23,588, szabadsági fok = 93, p = 0,0000). Bár a változó eloszlása ferde, az eltérés akkora, hogy nincsen szükség semmifajta robusztus tesztelésre.
Fontos megjegyezni, hogy ha kellenének a robusztus tesztek, akkor ott a fenti magyarázatban leírt statisztikák kellenek a hivatkozásba, illetve a leírásba. Több változó esetén az eredményeket összefoglaló táblázatban is be lehet mutatni, és a nyers szövegben már csak a különbségeket, illetve egyezéseket szükséges kiemelni.
A dolgozatokban tehát a változó ELOSZLÁSA dönti el, hogy az egymintás tesztek közül melyiket választjuk. A hivatkozásoknak minden esetben tartalmaznia kell a használt változó statisztikai jellemzőit. Ezek:
- T-próba, illetve annak robusztus változatai (Johnson és Gayen) esetén a t-érték, szabadsági fok és a p-érték.
- Wilcoxon-próba esetén mindenképpen szerepeljen, hogy ekkor már a mediánt teszteljük (ferde eloszlásnál nem alkalmazható), hivatkozni a z- és a p-értékre kell.
- Előjelpróba esetén (csak az ordinalitás kell hozzá, azaz ferde eloszlások esetén is használható) szintén a z- és p-érték kell.