3.7. Két csoportosító változó egyidejű hatásának tesztelése

3.7. Két csoportosító változó egyidejű hatásának tesztelése
Ebben az esetben azt vizsgálhatjuk, ha két csoportosító változó (nem, korcsoportok, lakóhelytípusok stb) figyelembevételével szeretnénk az adott változót megvizsgálni. Jelen esetben azt a módot követjük, hogy szeretnénk az IQ alapján övezetekre bontott populációnkban a nemeket megfigyelni a dominancia-változó mentén.
- Igaz-e, hogy a dominancia értéke másként viselkedik a férfiak és a nők között, amennyiben az IQ nagyságszintjét is figyelembe vesszük?
Ennek statisztikai megfogalmazása változatos, ugyanis egyszerre több dolgot is állítunk, egyszerre több dolgot is vizsgálunk. A legegyszerűbb talán azt megvizsgálni statisztikailag, ha ezt nem egyenlőséggel vagy függetlenséggel vizsgáljuk, hanem – kicsit kötve már a következő fejezet látásmódjához, egyfajta modellként szemléljük a változók kapcsolatát.
- Mit mondhatunk a dominancia-változó várható nagyságszintjéről, amennyiben a populációnkat nem- és intelligenciahányados-nagyság szerint szeretnénk csoportokba osztani?
Ez a szemlélet egyfajta modellt eredményez: milyen viszonyok írhatóak fel e 3 változó között. Természetesen ez magába foglalja, hogy nemenként, IQ-övezetenként is szemléljük a dominancia-változó nagyságszintjét, de egyben, egymás hatásait is figyelve szeretnénk értékelni a nagyságszinteket.
Ezt a feladatot könnyebb a ROPstat programban kiértékelni. A modell adta hipotézisek vizsgálatának feltételei a vizsgált változó normalitása, továbbá a már szinte megszokott szóráshomogenitás – azonban ez utóbbi vizsgálata és ellenőrzése nem annyira bonyolult, mint az összetartozó esetben. Amennyiben a normalitás sérül, úgy itt is érdemes a rangstatisztikai megfelelőket előszedni és futtatni.

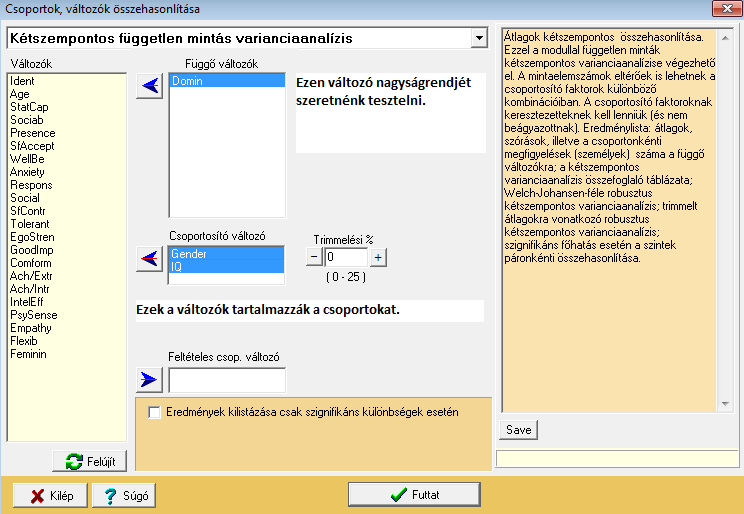
Ha minden beállításunk ilyen, úgy a következő eredményt nyerjük:
Független minták kétszempontos összehasonlítása
A beolvasott összes eset száma: 94
Jelölés: +: p < 0,10 *: p < 0,05 **: p < 0,01 ***: p < 0,001
1. csoportosító változó: Gender (Gender of subjects)
2. csoportosító változó: IQ (IQ of subjects)
Mintaelemszámok táblázata
| Gender | 'IQ' szerinti csoportok | ||||
| Index | csoport | low | middle | high | ÖSSZESEN |
| 1 | Male | 8 | 3 | 5 | 16 |
| 2 | Female | 19 | 37 | 22 | 78 |
| ÖSSZESEN | 27 | 40 | 27 | 94 | |
FÜGGŐ VÁLTOZÓ: Domin (Dominance)
Érvényes esetek száma: 82
Érvénytelen esetek száma: 12
AZ ÉRVÉNYES ESETEK KÉTSZEMPONTOS GYAKORISÁGI TÁBLÁZATA
| Gender | 'IQ' szerinti csoportok | ||||
| Index | csoport | low | middle | high | ÖSSZESEN |
| 1 | Male | 7 | 2 | 3 | 12 |
| 2 | Female | 15 | 34 | 21 | 70 |
| ÖSSZESEN | 22 | 36 | 24 | 82 | |
MINTAÁTLAGOK TÁBLÁZATA (Domin)
| Gender | 'IQ' szerinti csoportok | ||||
| Index | csoport | low | middle | high | ÁTLAG |
| 1 | Male | 12,29 | 10,00 | 12,00 | 11,43 |
| 2 | Female | 10,13 | 12,12 | 12,62 | 11,62 |
| ÁTLAG | 11,21 | 11,06 | 12,31 | ||
MINTASZÓRÁSOK TÁBLÁZATA (Domin)
|
|
'IQ' szerinti csoportok | |||
| Index | Gender | low | middle | high |
| 1 | Male | 4,608 | 4,243 | 4,583 |
| 2 | Female | 3,399 | 3,557 | 4,018 |
Varianciaanalízis összefoglaló táblázata (súlyozatlan átlagok módszere)
| Szóródás oka | f | Szórásnégyzet | F | p-érték | |
| Gender | 1 | 0,305 | 0,021 | 0,8844 | |
| IQ | 2 | 4,979 | 0,347 | 0,7077 | |
| Gende x IQ | 2 | 14,631 | 1,020 | 0,3653 | |
| Hibatag | 76 | 14,337 | |||
Szóráshomogenitás tesztelése -- Levene-próba: F(5; 76,0) = 0,332 (p = 0,8923)
Cellastatisztikák
| Index: | (1, 1) | (1, 2) | (1, 3) | (2, 1) | (2, 2) | (2, 3) |
| n: | 7 | 2 | 3 | 15 | 34 | 21 |
| Átlag: | 12,29 | 10,00 | 12,00 | 10,13 | 12,12 | 12,62 |
| Szórás: | 4,608 | 4,243 | 4,583 | 3,399 | 3,557 | 4,018 |
ROBUSZTUS kétszempontos varianciaanalízis (Domin)
- Welch-próba a Gender csoporthatás tesztelésére: F(1; 4,1) = 0,016 (p = 0,9044)
- Welch-próba az IQ csoporthatás tesztelésére: F(2; 3,3) = 0,210 (p = 0,6755)
- Johansen-próba a Gender x IQ interakció tesztelésére: Khi2(2) = 1,426 (p = 0,4901)
Az output elején láthatjuk a csoportok kategóriáit, illetve a különböző kategória-metszetekben számított szórásokat, átlagokat. Lényegében ezeket az átlagokat teszteljük, hogy egyenlők-e (főhatások), illetve azt, hogy ha nem egyenlők, akkor a főhatások egymástól függetlenül hatnak-e vagy sem (interakció).
Először tehát az output közepén található Levene-tesztet érdemes előszedni, hiszen ez dönti el, hogy majd a robusztus vagy a hagyományos eljárások közül kell választanunk. Az ott lévő F-érték és hozzá tartozó p-érték azt mutatja, hogy a szóráshomogenitás teljesül, tehát maradhatunk a hagyományos eljárásoknál.
A szóráshomogenitás-teszt feletti blokk mutatja, hogy a különböző főhatások, illetve a közöttük lévő interakció szignifikáns-e.
Minden sor elején láthatjuk, hogy főhatás (egy változó) vagy interakció (két főhatás keresztezése) kerül tesztelésre. A mellette látható érték a szabadsági fok, majd a megfelelő variancia (ezt analizáljuk, variancia = szórásnégyzet). Ezek után az F-érték és a hozzá tartozó p-érték.
Ezekből megállapítható, hogy egyik főhatás sem szignifikáns, továbbá az interakció sem kimutatható.
(Megjegyezzük, hogy az interakció annyit jelent, hogy a két szempont nem egymástól függetlenül fejti ki hatását – azaz a hatásuk nem egyszerűen összeadódik, hanem valamilyen gyengítés vagy erősítés történik a két változó valamely kombinációjában – az eredeti főhatás hatásokhoz képest).
Amennyiben a normalitás sérül, úgy rangstatisztikai eljárást is bevethetünk:
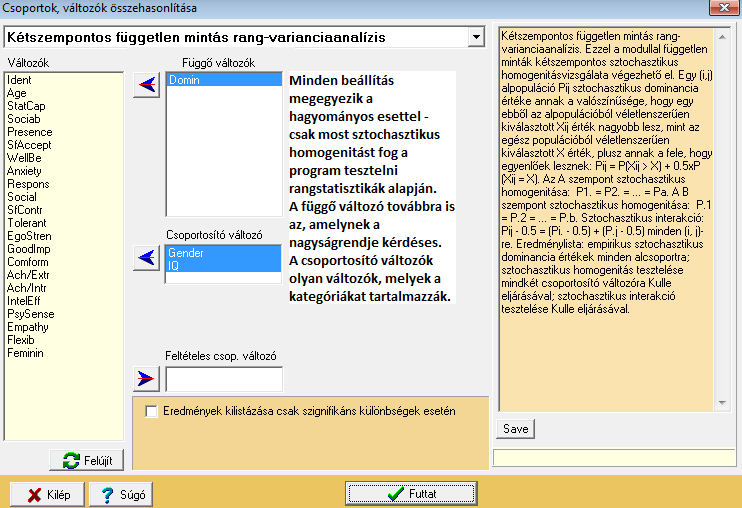
Ha minden beállítás helyes, a következő outputot kapjuk:
Független minták kétszempontos sztochasztikus összehasonlítása
A beolvasott összes eset száma: 94
Jelölés: +: p < 0,10 *: p < 0,05 **: p < 0,01 ***: p < 0,001
1. csoportosító változó: Gender (Gender of subjects)
2. csoportosító változó: IQ (IQ of subjects)
Mintaelemszámok táblázata
| Gender | 'IQ' szerinti csoportok | ||||
| Index | csoport | low | middle | high | ÖSSZESEN |
| 1 | Male | 8 | 3 | 5 | 16 |
| 2 | Female | 19 | 37 | 22 | 78 |
| ÖSSZESEN | 27 | 40 | 27 | 94 | |
FÜGGŐ VÁLTOZÓ: Domin (Dominance)
Érvényes esetek száma: 82
Érvénytelen esetek száma: 12
Átlagos mintaelemszám: n_átlag = 13,7
AZ ÉRVÉNYES ESETEK KÉTSZEMPONTOS GYAKORISÁGI TÁBLÁZATA
| Gender | 'IQ' szerinti csoportok | ||||
| Index | csoport | low | middle | high | ÖSSZESEN |
| 1 | Male | 7 | 2 | 3 | 12 |
| 2 | Female | 15 | 34 | 21 | 70 |
| ÖSSZESEN | 22 | 36 | 24 | 82 | |
A legkisebb mintaelemszám kisebb, mint 3.
Statisztikai elemzés nem végezhető.
A legkisebb mintaelemszám kisebb, mint 3.
Statisztikai elemzés nem végezhető.
Vegyük észre, hogy a program ezt nem tudja számunkra megoldani. Ezért újradefiniáljuk a csoportokat. A nem-változót nyilván lehetetlen átkódolni, azonban az IQ esetén a 3 csoport helyett csak kettőt fogunk engedni: lesz egy 120 alatti és egy 120 feletti csoport, így reménykedhetünk benne, hogy eredményes lesz a vizsgálat.
Az új beállításokkal az alábbi outputot nyertük:
Független minták kétszempontos sztochasztikus összehasonlítása
A beolvasott összes eset száma: 94
Jelölés: +: p < 0,10 *: p < 0,05 **: p < 0,01 ***: p < 0,001
1. csoportosító változó: Gender (Gender of subjects)
2. csoportosító változó: IQ (IQ of subjects)
Mintaelemszámok táblázata
| Gender | 'IQ' szerinti csoportok | |||
| Index | csoport | 0-120 | 121-200 | ÖSSZESEN |
| 1 | Male | 5 | 11 | 16 |
| 2 | Female | 14 | 64 | 78 |
| ÖSSZESEN | 19 | 75 | 94 | |
FÜGGŐ VÁLTOZÓ: Domin (Dominance)
Érvényes esetek száma: 82
Érvénytelen esetek száma: 12
Átlagos mintaelemszám: n_átlag = 20,5
AZ ÉRVÉNYES ESETEK KÉTSZEMPONTOS GYAKORISÁGI TÁBLÁZATA
| Gender | 'IQ' szerinti csoportok | |||
| Index | csoport | 0-120 | 121-200 | ÖSSZESEN |
| 1 | Male | 4 | 8 | 12 |
| 2 | Female | 10 | 60 | 70 |
| ÖSSZESEN | 14 | 68 | 82 | |
SZTOCHASZTIKUS DOMINANCIA ÉRTÉKEK TÁBLÁZATA (Domin)
| 'IQ' szerinti csoportok | |||
| Gender | 0-120 | 121-200 | ÁTLAG |
| Male | 0,595 | 0,444 | 0,519 |
| Female | 0,341 | 0,528 | 0,434 |
| ÁTLAG: | 0,468 | 0,486 | |
Sztochasztikus homogenitás (SZTH) elemzés (mintaelemszámokkal arányos populációsúlyok)
Kétszempontos rang-VA ÖSSZEFOGLALÓ TÁBLÁZATA (Domin)
| Hatás | Nullhipotézis | f1 | f2 | F | p-érték |
| Gender | Egyszempontos SZTH (A) | 1,0 | 78 | 0,715 | 0,4004 |
| IQ | Egyszempontos SZTH (B) | 1,0 | 78 | 0,031 | 0,8609 |
| Gend. x IQ | Nincs sztoch. interakció | 1,0 | 78 | 2,908 | 0,0921+ |
Jól láthatóan az előző esettel majdnem megegyező eredményt kaptunk – a rangstatisztika mutat egy tendencia-szintű interakciót, azonban szignifikáns eredményeket itt sem tudunk kimutatni.
Ilyen esetekben a válaszok némiképpen egyszerűsödnek, ráadásul minden módszer ugyanazt az eredményt hozta. Fontos azonban megjegyezni, hogy ehhez az elemzéshez, miután nem tartalmazza, érdemes a normalitás-vizsgálatot legalább előtte elvégezni a dominancia-változóra.
Műhelymunkabeli megfogalmazás
A kétszempontos (ANO)VA-elemzés esetén a feltételek ellenőrzése – ellentétben az összefüggő esettel – megtörténik, tehát meg kell emlékezni róla a dolgozatainkban is. A normalitás-vizsgálatot érdemes előtte lefuttatni – bár mi ezt most nagyvonalúan elhanyagoltuk, mert előzetesen már bemutattuk.
A dominancia vizsgálata nemenként és az IQ különböző kategóriái mentén
A dominancia-változót mind férfiak és nők, mind pedig az IQ három (rangstatisztikákkal kettő) kategóriájában számítottuk, értékeltük.
Az egymáshoz való viszonyuk alapján kijelenthető, hogy sem a rangstatisztikák, sem a hagyományos eljárások nem mutattak szignifikáns eltéréseket (a legkisebb p-értéket a rangstatisztika interakciója esetén tapasztaltuk, p>0,09).
Ez alapján kijelenthető tehát, hogy sem a nem szerinti megkülönböztetés, sem az IQ eltérései nincsenek hatással a dominancia-skálán várható értékre.
Természetesen akkor, ha valakinek a dolgozatában ez a fő csapásvonal, akkor a különböző átlagok, szórások, minden egyéb statisztika külön-külön kiemelhető és tárgyalható, magyarázva, hogy miért is nincsenek nem vagy intelligencia alapján meghatározható különbségek a dominancia-változó várható értékében.
Ezeket egyénileg érdemes interpretálni, azokra az esetekre, helyzetekre koncentrálva, melyek számunkra fontosak.