3.6. Legalább 3 összetartozó mintát tesztelünk

Ebben a fejezetben olyan kérdéseket tárgyalunk, amikor összetartozó mintákkal dolgozunk (pl. ugyanazon csoport legalább 3 különböző időpontban mért adatai, vagy összefüggő változók azonos csoportban mérve). Egy lehetséges szakmai hipotézis lehet a következő:

Igaz-e, hogy a Szondi-tesztben a több szadista kép megítélése azonos?

Ismét olyan megfogalmazásunk van, mely statisztikai hipotézis is egyben, hiszen ismét egyenlőséget tesztelhetünk.

Ebben az esetben is feltétel a normalitás, azonban a szóráshomogenitás-feltétele ennek az esetnek lényegesen bonyolultabb, mint a független eseté. Ez az úgynevezett szfericitási feltétel elég bonyolult számításokkal végezhető csak el – viszonylag ritkán is teljesül – így érdemes rögtön robusztus eljárásokat is figyelembe venni. Ennek következtében érdemes ezen eljárásokat automatikusan a robusztus tesztekkel ellenőrizni.

Ráadásul az intervallum-skálatípus beállítása itt is automatikusan tartalmazza az outputban a rangstatisztikai eljárásokat.

Kettőnél több összetartozó minta nagyságszintjének tesztelése – ROPstat programcsomagban

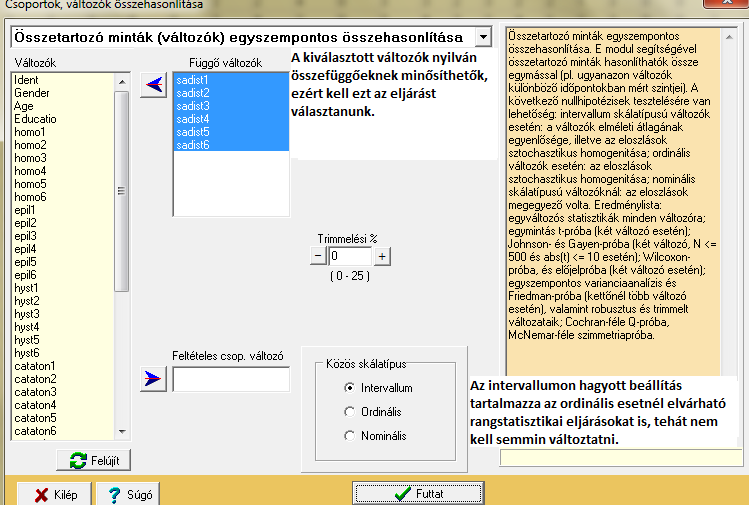
Amennyiben ezeket a beállításokat használjuk, a következő outputot nyerjük:

Összetartozó minták egyszempontos összehasonlítása

FÜGGÓ VÁLTOZÓK:

sadist1

sadist2

sadist3

sadist4

sadist5

sadist6

A beolvasott összes eset száma: 277

Érvényes (komplett) esetek száma: 277

Jelölés: +: p < 0,10 *: p < 0,05 **: p < 0,01 ***: p < 0,001

Elméleti átlagok egyenlőségének tesztelése:

- Varianciaanalízis (VA): F(5,1380) = 96,412 (p = 0,0000)***

(Hatásvariancia = 113,3921, Hibavariancia = 1,1761)

- Robusztus VA szabadságfok-korrekcióval

Geisser-Greenhouse (epszilon = 0,927): F(4,6; 1278,8) = 96,412 (p = 0,0000)***

Huynh-Feldt (epszilon = 0,944): F(4,7; 1303,3) = 96,412 (p = 0,0000)***

Sztochasztikus homogenitás tesztelése:

- Friedman-próba: G(5) = 352,332 (p = 0,0000)***

- Rangszámokon végzett VA: rF(5,1380) = 94,594 (p = 0,0000)***

- Robusztus rang-VA szabadságfok-korrekcióval

Geisser-Greenhouse (epszilon = 0,955): rF(4,8; 1318,4) = 94,594 (p = 0,0000)***

Huynh-Feldt (epszilon = 0,974): rF(4,9; 1344,5) = 94,594 (p = 0,0000)***

Index	Változó	Átlag	Szórás	Rang-átlag	Sztochasztikus dominancia
1.	sadist1	1,282	1,080	2,88	0,376***
2.	sadist2	1,451	1,320	3,05	0,411***
3.	sadist3	2,437	1,100	4,47	0,694***
4.	sadist4	2,690	1,244	4,74	0,748***
5.	sadist5	1,329	1,020	2,92	0,383***
6.	sadist6	1,296	1,014	2,94	0,388***

Megjegyzés:

Minden változó esetében a sztochasztikus dominancia annak a valószínűségét jelzi,

hogy ennek a változónak egy véletlen értéke (Xj) nagyobb lesz, mint egy random

megfigyelés bármely változótól (X), plusz az egyenlőség valószínűségének a fele:

SZTDj = P(Xj > X) + 0,5P(Xj = X)

A sztochasztikus homogenitás definíciója: SZTD1 = SZTD2 = SZTD3 = ... = 0,5

Egy SZTDj érték szignifikanciája azt jelenti, hogy a Hj: SZTDj = 0,5 hipotézis elvethető.

Átlagok Tukey-féle páronkénti összehasonlítása (k = 6, df = 1380):

T12= 2,60 T13= 17,73** T14= 21,61** T15= 0,72 T16= 0,22 T23= 15,13** T24= 19,00**

T25= 1,88 T26= 2,38 T34= 3,88+ T35= 17,01** T36= 17,51** T45= 20,89** T46= 21,39**

T56= 0,50

Rangátlagok Tukey-féle páronkénti összehasonlítása (k = 6, df = 1380):

T12= 1,96 T13= 17,95** T14= 20,96** T15= 0,41 T16= 0,65 T23= 15,99** T24= 19,01**

T25= 1,55 T26= 1,30 T34= 3,01 T35= 17,54** T36= 17,29** T45= 20,55** T46= 20,31**

T56= 0,24

Jól látható, hogy mind a varianciaanalízis, mind annak robusztus változatai, mind a rangstatisztikán alapuló sztochasztikus dominancia tesztelések azt mutatják, hogy e kérdések között vannak különbségek, vannak kiemelkedő képek, melyek kedveltsége valamilyen módon eltér a többiétől.

Az eljárásunk feltételeinek ellenőrzése bonyolult, így inkább a robusztus változatokat figyeljük: miután a számított statisztika melletti p-érték mindenhol 0,0000, ezért bizton állíthatjuk, hogy e képek kedveltsége nem egyenlő.

A páros összehasonlítások között (Tukey, alsó két blokk) megfigyelhetjük, hogy pl. az első két kép között (T12) nem látunk szignifikáns különbséget, azonban ha azokat az eseteket figyeljük, ahol a 3-as vagy 4-es kód szerepel, akkor jól látható, hogy ez a két kép csak egymástól nem különbözik, minden más képtől eltérést mutat.

Ennek kapcsán megállapítható, hogy – miután a többi kép között eltéréseket, *-al jelzett különbségeket nem vehetünk észre – az 1-2-5-6. képek kedveltsége között nincsen eltérés, míg a 3-4. képek ezeknél szignifikánsan magasabb értékeken szerepelnek, ráadásul a 3-4. képek között sem találhatunk szignifikáns különbséget.

Műhelymunkabeli megfogalmazás

Az összetartozó mintás ANOVA esetén is kiemelhető a teljes különbség tesztelése, illetve az egyenkénti, páros különbségek összehasonlítása. Azonban fontos megemlíteni, hogy itt a feltételeket nem tudjuk ellenőrizni, ezért érdemes lehet rögtön a robusztus tesztekre hivatkozni, a feltételek ellenőrzésének okait is megemlítve!

A sadist képek kedveltségének összehasonlítása

A 6 képet egyszerre vizsgálva az eljáráshoz fontos normalitási és szfericitási feltételek ellenőrzésének nehézsége miatt rögtön robusztus és rangstatisztikai eljárásokat fogunk figyelembe venni (főleg azért, mert a fenti eljárásban lévő változók 5 fokozatú Likert-skálán értékelt változók, tehát a normalitás „megkérdőjelezhető” lenne).

Mind a hagyományos, mind a normalitást feltételező, de robusztus eljárás azt mutatja, hogy (F(5,1380) = 96,412 (p = 0,0000)***) szignifikáns eltérés van (robusztus, Huynh–Feldt (epszilon = 0,974): rF(4,9; 1344,5) = 94,594 (p = 0,0000)***).

Mindezt megerősítik a rangstatisztikai eljárások, melyek sztochasztikus dominanciát mutatnak:

Friedman, G(5) = 352,332, p=0,0000*, illetve Huynh–Feldt (epszilon = 0,974): rF(4,9; 1344,5) = 94,594 (p = 0,0000)***.

Ezek után páros összehasonlításokat végeztünk, ahol a Tukey-féle összehasonlítások alapján elmondható, hogy az 1-2-5-6. képek értékei egymástól nem térnek el. Szintén nem térnek el szignifikánsan a 3-4. képek értékei egymástól, azonban az első csoportba sorolt képek szignifikánsan alacsonyabb értékeket kaptak, mint a 3-4. képek.

A páros összehasonlítások adott esetben táblázatos formában is megjeleníthetők vagy valamilyen diagramon ábrázolhatók. Ennek megvalósítására több program is alkalmas, érdemes lehet vele kísérletezni – de ez már nem tartozik szigorúan a matematikai statisztikai problémák közé.