4. Kvantitatív változók közötti kapcsolatvizsgálat

4. Kvantitatív
változók közötti kapcsolatvizsgálat
Korábban már ígértem, hogy a VA során tapasztalt egyik output-elemre vissza fogunk térni. A VA esetén láthatunk egy nemlineáris korrelációs együtthatót és egy eta-négyzetet. Ezek nem mások, mint a lineáris regresszióból, illetve Pearson-féle korrelációs együtthatóból általánosított mutatók.
A determinációs együttható vagy magyarázott variancia-arány általánosítása jelenik meg a középértékek összehasonlításakor a ROPstat outputján, amikor nemlineáris magyarázott variancia-arány mutatókat közöl a program (eta-négyzet).
- Vizsgáljuk meg mindkét programban a dominancia és a szociabilitás kapcsolatát.
Ennek az eljárásnak a sajátossága – az e leírásban szereplő többi eljárással szemben – hogy nincsen szigorúan vett feltétele, hiszen itt modellt írunk fel. Azt kell tudnunk, hogy ebben az esetben pl. lineáris regressziót alkalmazunk, azaz a két változó között egy lineáris kapcsolatot fog keresni az eljárás.
Magyarán: csak azt akarjuk most eldönteni, hogy van-e LINEÁRIS (monoton) kapcsolat a két változó között. Azonban tudnunk kell, hogy ha a két mért változó normális eloszlású, akkor közöttük csak és kizárólag lineáris kapcsolat lehet, tehát normális eloszlású változók körében a lineáris kapcsolat megléte vagy hiánya ekvivalens a meglévő vagy hiányzó kapcsolattal a két változó között.
Ezt az eljárást mind ROPstatban, mind SPSS-ben megnézzük, azonban SPSS-ben két külön eljárást kell majd futtatni, hogy a ROPstattal azonos outputot kaphassunk.
Korrelációs együttható(k) és egyszerű lineáris regresszió – ROPstat programcsomagban
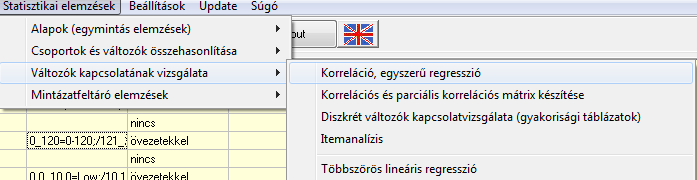
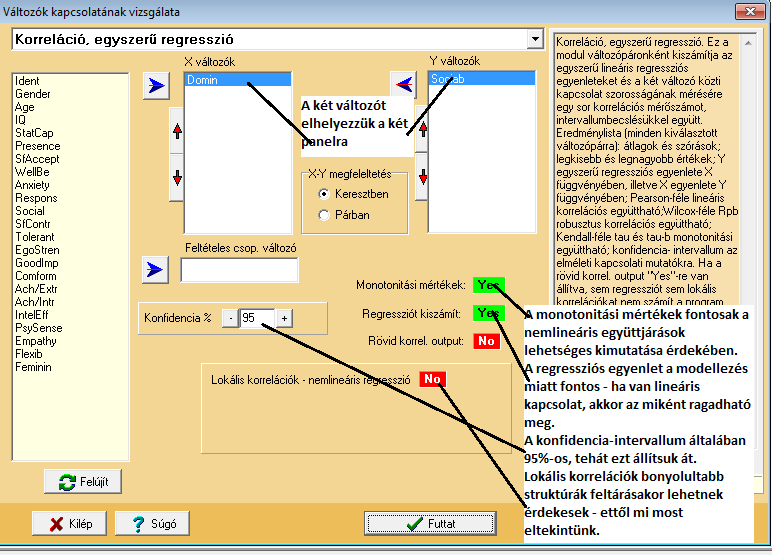
Amennyiben ilyen beállításokat használunk, a következő outputot
nyerjük:
Korreláció, lineáris regresszió
A beolvasott összes eset száma: 94
Jelölés:
r: Pearson-féle lineáris korrelációs együttható
Rpb: Wilcox-féle robusztus korrelációs
együttható
Tau-b: Kendall-féle tau-b monotonitási
együttható
Tau: Kendall-féle tau monotonitási együttható
p_pos: Pozitív együttjárás (konkordancia)
százaléka
p_neg: Negatív együttjárás (diszkordancia)
százaléka
Szignifikancia: +: p < 0,10 *: p < 0,05
**: p < 0,01 ***: p < 0,001
ELEMZENDŐ VÁLTOZÓPÁR:
X = Domin (Dominance)
Y = Sociab (Sociability)
A mind X, mind Y esetében érvényes értékkel rendelkező esetek
száma: N = 82
| Változó | Átlag | Var. | Min. | Max. | Regressziós egyenlet | |
| X: | Domin | 11,84 | 14,28 | 4 | 20 | x = 0,779 + 0,757y |
| Y | Sociab | 14,62 | 11,52 | 7 | 21 | y = 7,395 + 0,610x |
X: Reziduális variancia (Hibavariancia): MSerr(X) = 7,688, SH(X)
= 2,773
Y: Reziduális variancia (Hibavariancia): MSerr(Y) = 6,202, SH(Y) =
2,490
Korrelációk és 95%-os intervallumbecslés az elméleti értékre:
| r = | 0,680*** | p = 0,0000 | C95 = (0,5454; 0,780) |
| Rbp = | 0,674*** | p = 0,0000 | C95 = (0,539; 0,776) |
| tau-b = | 0,518*** | p = 0,0000 | C95 = (0,360; 0,677) |
| tau = | 0,487*** | p = 0,0000 | C95 = (0,330; 0,625) |
p_poz = 66,6%, p_neg = 18,8%
A korreláció és regresszió esetén lényegében egyetlen hipotézist
kell vizsgálnunk: van-e szignifikáns kapcsolat vagy nincsen? Ezt az
output legalsó blokkjában tudjuk ellenőrizni – minden egyéb csak
azután érdekes, hogy szignifikáns kapcsolatot látunk (nem tudunk
modellt értelmezni, ha nincs is kapcsolat).
Azt láthatjuk, hogy mind a Pearson-féle korrelációs együttható ’r’, mind annak robusztus változata, mind pedig a két Kendall-féle tau-mutató szignifikánsan eltér a 0-tól, mindegyik pozitív és közepesen erős (az első kettő lineáris, az utóbbi kettő monoton) kapcsolatot jelez.
Az egyenletekből megállapítható, hogy a dominancia és a szociabilitás miként fejezhetőek ki egymásból.
Korrelációs együttható(k) és egyszerű lineáris regresszió – SPSS programcsomagban
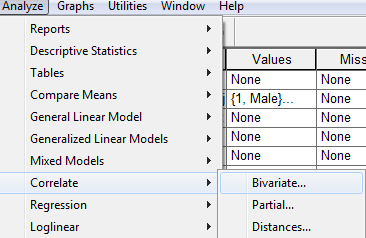
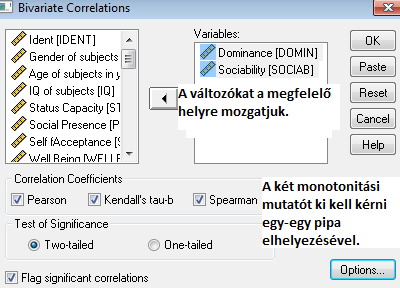
Amennyiben szeretnénk regressziós egyenletet is, úgy egy másik eljárást is futtatnunk kell még – ez ugyanis csak a következő outputot adja:
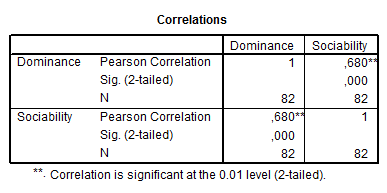
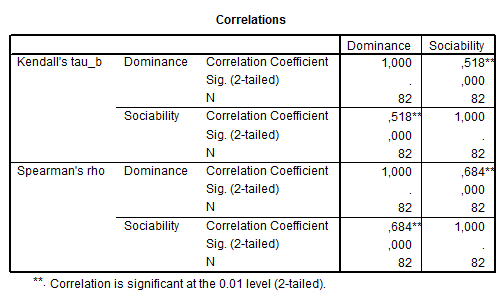
A ROPstathoz hasonlóan itt is látható, hogy közepesen erős, szignifikáns kapcsolatot talált a szociabilitás és a dominancia között. Minden eredmény megegyezik a ROPstat eredményeivel – csak az egyenleteket nem látjuk még, mert azt egy másik menüpontból kell lekérnünk.
A lineáris regresszió a következő módon érhető el az SPSS-ben:
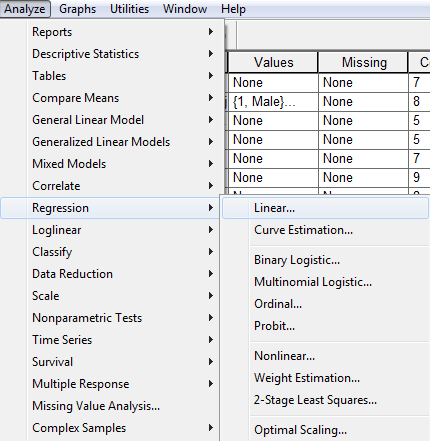
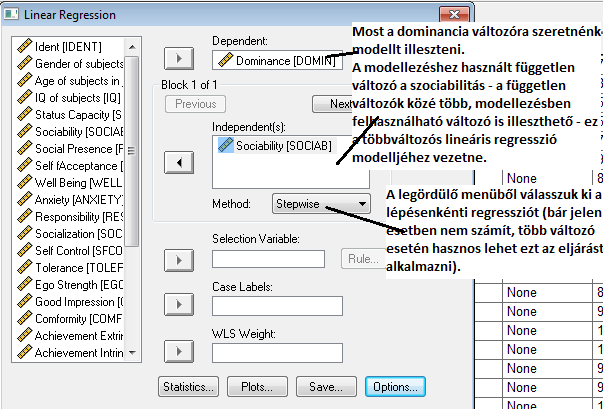
Amennyiben mindent helyesen állítottunk be, az alábbi outputot
kapjuk:
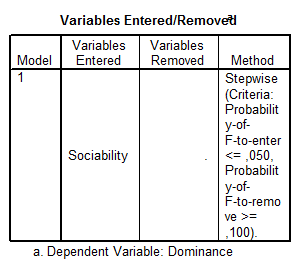
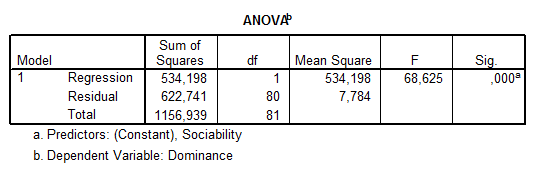
A modell szignifikanciáját a 3. táblázat (ANOVA) F-statisztikájának szignifikanciája mutatja meg számunkra. Amennyiben itt a Sig.-érték 0,05 alatti, úgy van értelme tovább foglalkozni a regressziós modellel (amennyiben a fenti, stepwise-algoritmust használjuk, úgy csak szignifikáns modellt láthatunk).
Az első táblázatot csak többváltozós esetben szokás érdemben vizsgálni, ugyanis ebben a táblázatban kerülnek felsorolásra a modellbe bevont változók. Itt most a dominancia-változóra nyilván a szociabilitás-változót vontuk be.
Az F-érték alapján tehát szignifikáns kapcsolat van a változóink között, a korrelációs együttható 0,68 (közepesen erős, pozitív kapcsolat) és az ebből számított determinációs együttható (r-négyzet) 0,46.
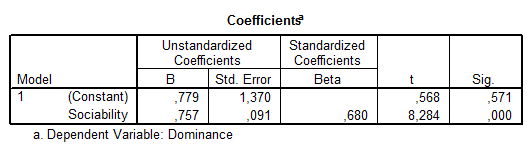
A felírható modell:
- 0,779 + 0,757*szociabilitás = dominancia
A másik lehetőség a modell ellenőrzésére: ha a modell felírására használt utolsó táblázatban vizsgáljuk az együtthatók szignifikanciáját (azt vizsgáljuk, hogy az együttható 0 vagy nem 0). Hiszen amennyiben 0 lenne az együttható, akkor feleslegesen írjuk fel a modellbe.
Műhelymunkabeli megfogalmazás
A szociabilitás- és dominancia-változók kapcsolata
A két változó között szignifikáns, pozitív, közepesen erős kapcsolat van (r = 0,68, p = 0,0000). A magyarázott variancia-arány 0,46 (46%). Megállapítható tehát, hogy a szociabilitás növekedésével a dominancia növekedése jár együtt.
Figyeljünk oda arra, hogy az ilyen esetekben MINDIG először a szignifikanciát ellenőrizzük. Nem mondhatunk semmit sem a modellről, ha nincsen szignifikáns viszony – tehát bármely számított paraméterrel csak akkor van értelme foglalkoznunk, ha meglévő kapcsolatot látunk.