5. Diszkrét változók közötti kapcsolatvizsgálat

Diszkrét változók közötti kapcsolatvizsgálat esetén egy előző fejezetben már tárgyalt kapcsolatvizsgálatot veszünk elő – más köntösbe bújtatva.

A kétmintás t-próbát használtuk arra, hogy a feminitás nagyságszintjét férfiak és nők között összehasonlíthassuk.

Most is hasonló dolgot fogunk tenni - a nem és az IQ kapcsolatát fogjuk vizsgálni. Alapesetben ez egy kétmintás t-próba lenne, azonban ha övezetes felírása is létezik a folytonos változónak, akkor ránézhetünk úgy is, hogy alacsony, közepes és magas IQ-szint, melyeknek van-e kapcsolata a nem-változóval?

Van-e kapcsolat a nem és az IQ között?

Statisztikai hipotézisként az alábbi vizsgálatot fogjuk végrehajtani:

Az IQ- és a nem-változók függetlenek egymástól.

Ennek az eljárásnak egyetlen feltétele van, melynek ellenőrzése be van építve mindkét programcsomagba: az elvárt vagy várható gyakoriságoknak minden egyes cellában (a kereszttábla minden kategória-párosításában) legalább 5-nek kell lennie. Ez alól kis kivételt tehetünk: amennyiben a cellák legalább 80%-ában ezt elértük, úgy alkalmazható az eljárás (tehát 2 x 2-es esetben minden cella, de 2 x 3 cella esetén pl. 1 cellában sérülhet e feltétel).

A 2 x 2-es eset specifikus, ugyanis ebben az esetben használható az úgynevezett Fisher-egzakt próba, melynek nincsen feltétele: bármikor alkalmazható, bármilyen cellagyakoriság esetén – azonban csak 2 x 2-es esetekre.

Kereszttáblás elemzések – ROPstat programcsomagban

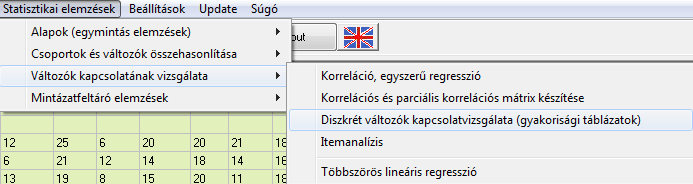
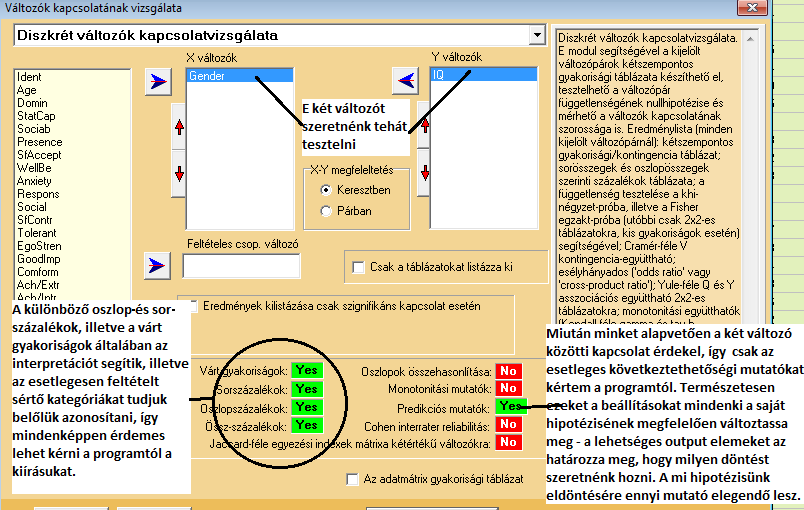
Ha mindent a fentiek szerint állítottunk be, úgy a következő outputot kapjuk:

Diszkrét változók kapcsolatvizsgálata

Jelölés: +: p < 0,10 *: p < 0,05 **: p < 0,01 ***: p < 0,001

A beolvasott összes eset száma: 94

KÉTSZEMPONTOS GYAKORISÁGI TÁBLÁZAT

Sorváltozó: Gender (Gender of subjects)

Oszlopváltozó: IQ (IQ of subjects)

	Az IQ változó csoportjai/kategóriái:
Gender	low	middle	high	Összesen
Male	8	3	5	16
Female	19	37	22	78
Összesen	27	40	27	94

Várt gyakoriságok táblázata

	Az IQ változó csoportjai/kategóriái:
Gender	low	middle	high	Összesen
Male	4,616	6,8	4,6	16
Female	22,4	33,2	22,4	78
Összesen	27	40	27	94

Sorösszegek szerinti százalékok táblázata

	Az IQ változó csoportjai/kategóriái:
Gender	low	middle	high	Összesen
Male	50,0	18,8	31,3	100,0
Female	24,4	47,4	28,2	100,0
Összesen	28,7	42,6	28,7	100,0

Oszlopösszegek szerinti százalékok táblázata

	Az IQ változó csoportjai/kategóriái:
Gender	low	middle	high	Összesen
Male	29,6	7,5	18,5	17,0
Female	70,4	92,5	81,5	83,0
Összesen	100,0	100,0	100,0	100,0

Kétszempontos százalékos gyakoriságok táblázata

	Az IQ változó csoportjai/kategóriái:
Gender	low	middle	high	Összesen
Male	8,5	3,2	5,3	17,0
Female	20,2	39,4	23,4	83,0
Összesen	28,7	42,6	28,7	100,0

KAPCSOLATI MUTATÓK

Cramér-féle kontingencia-együttható, V = 0,245

Goodman-Kruskal-féle predikciós mutatók

A) Mind a sor-, mind az oszlopváltozó véletlen változónak tekinthető:

- Oszlopváltozó predikciója a sorváltozó alapján:

Lambda(oszlop|sor) = 0,093, Tau(oszlop|sor) = 0,032

- Sorváltozó predikciója az oszlopváltozó alapján:

Lambda(sor|oszlop) = 0,000, Tau(sor|oszlop) = 0,048

B) Csak a bejósolandó változó tekinthető véletlen változónak:

- Oszlopváltozó predikciója a sorváltozó alapján:

Lambda*(oszlop|sor) = 0,184, Tau*(oszlop|sor) = 0,056

- Sorváltozó predikciója az oszlopváltozó alapján:

Lambda*(sor|oszlop) = 0,000, Tau*(sor|oszlop) = 0,054

Közös információ-hányad

- Oszlopváltozó predikciója a sorváltozó alapján: UC(oszlop|sor) = 0,028

- Sorváltozó predikciója az oszlopváltozó alapján: UC(sor|oszlop) = 0,067

FÜGGETLENSÉG TESZTELÉSE

Khi-négyzet-próba (f = 2): Khi2 = 5,649 (p = 0,0593)+

FIGYELEM: Túl sok az 5-nél kisebb várt gyakoriságok száma: k = 2

Emiatt a khi-négyzet-próba érvényessége kétséges lehet.

A kereszttáblás elemzések során a leíró statisztikai részekhez tartoznak a különböző táblázatok: tapasztalati gyakoriságok, százalékos eloszlások – sor- és oszlopösszeg szerint, illetve a teljes százalékos megoszlás.

A predikciós mutatók és egyéb mutatók akkor értelmesek, ha az egész elemzéshez tartozó khi-négyzet statisztika (mely a függetlenség-tesztelés elnevezésű, utolsó blokkban található) szignifikáns. Esetünkben ezzel több gond is adódik, mert egyik oldalról a várható gyakoriságok nem elég nagyok (le tudjuk ellenőrizni, hogy 2 cellában is 5 alatti értéket kapunk), másik oldalról pedig az érték csak tendencia-szintű. Tehát elmondható, hogy az IQ- és a nem-változók szignifikánsan nem függenek egymástól. Természetesen ez azt jelenti, hogy a predikciós mutatók (valaki neméből előre tudnánk-e jelezni az IQ-ját?), illetve a kapcsolat erősségét mérő kontingencia-együtthatók nem magyarázhatók.

Kereszttáblás elemzések – SPSS programcsomagban

Az SPSS programcsomagnak ez a fejezete a leíró statisztikáknál található meg (ne keverjük össze a nemparaméteres statisztikák khi-négyzet-próbájával).

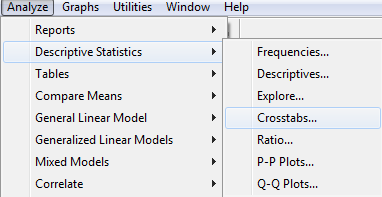
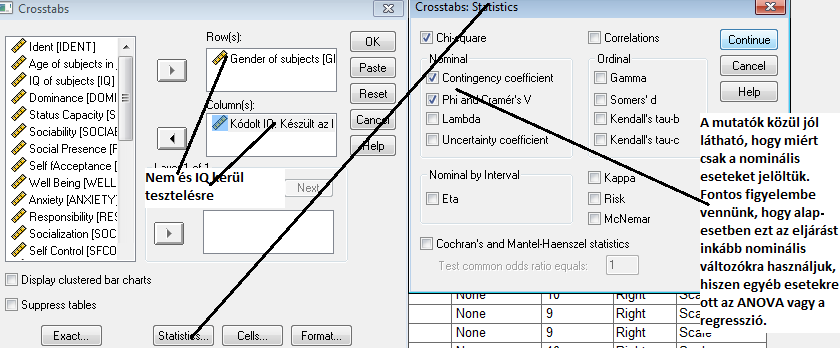
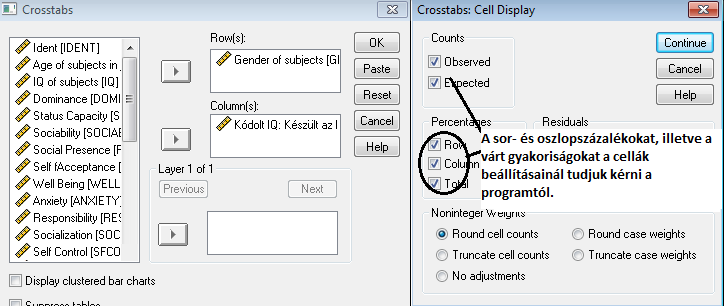
Ezen beállításokkal az alábbi táblázatokat, outputot nyerjük:

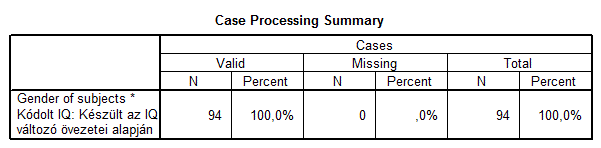
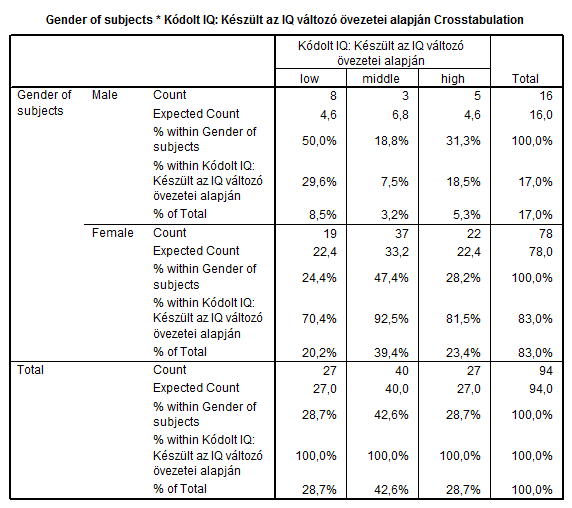
Az első táblázatban a hiányzó adatok számát követhetnénk nyomon. A második táblázatban látható EGYBEN az a négy táblázat, ami a ROPstat sor-/oszlop-/teljes százalékos megoszlása, illetve várható eloszlása (blokkonként: tapasztalt, várható, sor-, oszlop- és teljes %).

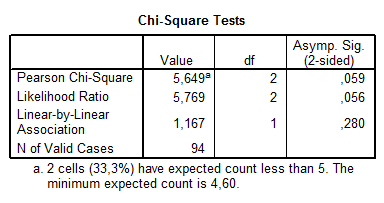
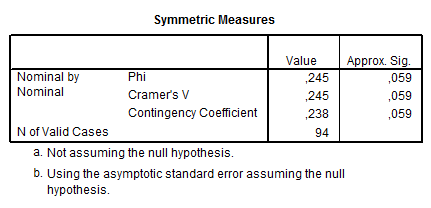
Az utolsó előtti táblázat tartalmazza a megfelelő khi-négyzet statisztikát, majd az utolsó táblázat a belőle képezett, kapcsolat erősségét mérő kontingencia-együtthatókat.

Ezek alapján is az mondható el, hogy nincsen szignifikáns kapcsolat a nem és az IQ között.

Műhelymunkabeli megfogalmazás

A nem- és az IQ-változó kapcsolata

A két változó között nem tapasztalható szignifikáns összefüggés (khi-négyzet = 5,649, Sig. = 0,059). Ráadásul a várt gyakoriságok miatt ez az érték megbízhatatlannak is tűnik, hiszen túl sok cellában (2) sérült a próba feltétele. Az eredményünket úgy is interpretálhatjuk, hogy valaki neméből nem tudunk az intelligenciahányadosának mértékére, pontosabban annak nagyságszintjére következtetni.

Figyeljünk oda arra, hogy az ilyen esetekben MINDIG először a szignifikanciát ellenőrizzük! A kontingencia-együttható nagyságszintje nem mond semmit olyan esetekben, amikor a khi-négyzet statisztika alapján a függetlenség nem elvethető.