3.2. Egy változó nagyságszintjének tesztelése 2 csoportban

3.2. Egy változó nagyságszintjének tesztelése 2 csoportban
Egy változó nagyságszintjének tesztelése 2 csoportban
Ebben a fejezetben olyan kérdéseket tárgyalunk, amikor két csoport (akár kontroll- és vizsgálati csoportok összehasonlítása, akár két független csoport, mint férfiak-nők) kerül összehasonlításra valamely vizsgált változó mentén. A kérdésfelvetés szakmailag többek között az alábbi módon fogalmazható meg:
- Igaz-e, hogy a férfiak feminitás-értéke alacsonyabb, mint a nőké?
Világos az előző fejezet alapján, hogy e fenti kérdés szakmai hipotézis – statisztikailag nem ezt fogjuk vizsgálni, tesztelni, hanem:
- Igaz-e, hogy a férfiak és nők feminitás-értékének mértéke megegyezik?
Vegyük észre, hogy – az előző fejezetben már hangsúlyt kapott módon – itt e hipotézist már szándékosan nem is az átlagon keresztül fogalmazzuk meg, bár megtehetnénk. A hagyományos eljárás (kétmintás t-próba) alkalmazásához két feltételt kell teljesítenünk: a vizsgált változónknak (jelen esetben a feminitásnak) normális eloszlásúnak kell lennie, továbbá a két csoportban e mért változó szórása nem különbözhet egymástól.
A két feltétel közül a normalitás (ahogy már az egymintás esetben is) nagyobb minták esetén nem számít szigorú feltételnek (nagyobb mintának mondjuk 100 főt vehetünk), azonban a szórások egyezése (ez az úgynevezett szóráshomogenitás) igen fontos kitétele a hagyományos eljárás alkalmazásának.
Amennyiben ez sérül, úgy robusztus alternatívát kell nézni az átlag tesztelésére (tehát ekkor a normalitás még fennáll) – ez lesz a Welch-féle d-próba.
Amennyiben kisebb mintánk van, vagy úgy érezzük, hogy az átlag nem megfelelő mutató a számunkra, mert pl. két ellentétesen ferde eloszlásról van szó, úgy az úgynevezett Mann–Whitney-statisztikát, illetve egyéb, robusztus rangstatisztikai módszereket lehet bevetni – ám ekkor már sztochasztikus egyenlőséget tesztelünk.
A ROPstatban ezeket a problémákat végigvesszük, az SPSS-ben a hagyományos kétmintás t-próbát, a Welch-féle d-próbát és a Mann-Whitney-statisztikát fogjuk megnézni.
Egy változó nagyságszintjének tesztelése 2 csoportban – a ROPstat programcsomagban
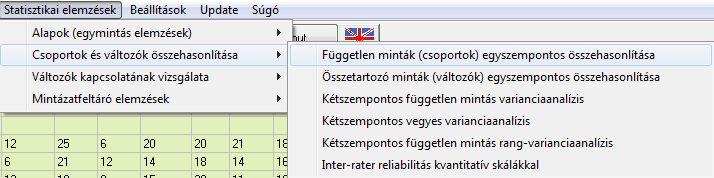
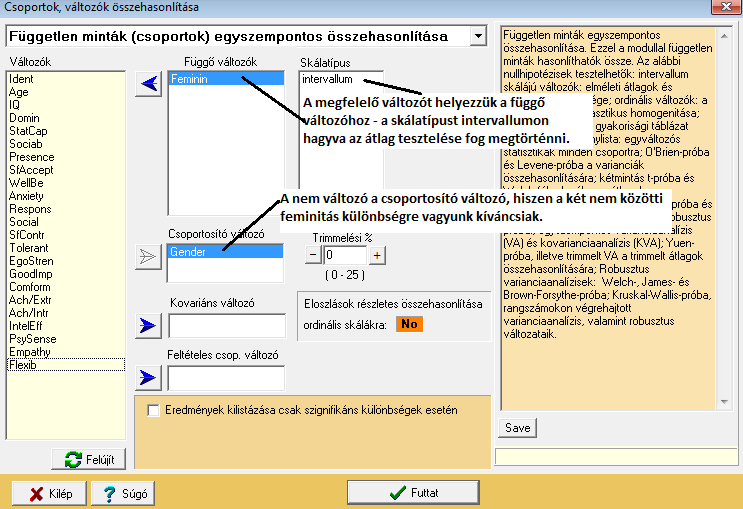
Amennyiben ezt a beállítást használjuk, úgy az átlagokat teszteljük, és az alábbi outputot nyerjük:
A beolvasott összes eset száma: 94
Csoportosító változó: Gender (Gender of subjects)
Jelölés: +: p < 0,10 *: p < 0,05 **: p < 0,01 ***: p < 0,001
FÜGGŐ VÁLTOZÓ: Feminin (Femininity)
Csoportonkénti alapstatisztikák
| Index | Gender | Esetek | Átlag | Szórás | Min. | Max. | Ferdeség | Csúcsosság |
| 1 | Male | 12 | 12,08 | 2,678 | 8 | 16 | 0,268 | -1,241 |
| 2 | Female | 70 | 14,00 | 1,963 | 10 | 18 | 0,154 | -0,465 |
Ha a Ferdeség vagy a Csúcsosság szignifikáns, az a normalitás sérülését jelzi.
Elméleti szórások egyenlőségének tesztelése
- O'Brien-próba (Welch-féle): F(1,0; 12,9) = 2,604 (p = 0,1308)
- Levene-próba (Welch-féle): F(1; 14,6) = 3,409 (p = 0,0852)+
Elméleti átlagok egyenlőségének tesztelése
Hagyományos eljárás, amely feltételezi a szóráshomogenitást:
- Kétmintás t-próba: t(80) = -2,954 (p = 0,0041)**
Hatásvariancia = 37,6321, Hibavariancia = 4,3115
Korrelációs hányados (nemlineáris korrelációs együttható): eta = 0,314
Megmagyarázott variancia-arány: eta-négyzet = 0,098
Cohen-féle delta hatásmérték: d = -0,923
Robusztus eljárás, amelynél nem szükséges a szóráshomogenitás:
- Welch-féle d-próba: d(13,1) = -2,372 (p = 0,0337)*
95%-os konfidencia-intervallum a két elméleti átlag m1-m2 különbségére
- a kétmintás t-próba alapján: C(0,95) = (-3,210, -0,623)
- a Welch-féle d-próba alapján: C(0,95) = (0,028; 0,599)
Az output szerkezete a következő: először az esetszám és a csoportosító változó van feltüntetve, majd a már megismert, szignifikanciákat jelölő * és + jelek.
Ezek után a vizsgálathoz szükséges alapstatisztikák következnek – az átlagokat teszteljük, a szórások egyezése az egyik feltétel (ezért kellenek a szórások), illetve a normalitás a másik (ferdeség és csúcsosság). Amennyiben a ferdeség és csúcsosság szignifikánsan eltér valamely csoportban a 0-tól, úgy ott + vagy * jel lesz látható – most ezzel nincsen gondunk.
Az első teszt a szórások egyezésének tesztelése Levene- vagy O’Brien-próbával, melyek a szóráshomogenitásnak robusztus tesztjei. Hivatkozni az F-értékekre, a zárójelekben lévő szabadsági fokokra és a p értékekre kell – itt egyik esetben sem látunk *-ot, tehát nincsen szignifikáns különbég a szórások között.
Így – miután mindkét feltétel teljesül – használhatjuk az első blokkban lévő hagyományos eljárást, a kétmintás t-próba lesz számunkra az érdekes. Azt láthatjuk, hogy a t-érték megfelelően eltér 0-tól, a p-érték alapján ez az eltérés szignifikáns, tehát a két átlag között szignifikáns különbség van. Jelen esetben a hatásvariancia és egyéb paraméterek nem számítanak – a későbbiekben, a korrelációs együtthatók vizsgálatakor erre ki fogunk térni.
Amennyiben a szóráshomogenitás tesztelésekor gond lenne, úgy a következő blokkot kéne nézni, a Welch-féle d-próbát (hivatkozás: t-értékre, szabadsági fokra és p-értékre). Ez is azt mutatja, hogy szignifikáns eltérés van a két átlag között.
A konfidencia-intervallum a különbségre nem fontos számunkra.
Amennyiben a nagyságszinti viszonyok érdekelnek minket – tehát nem az átlagot szeretnénk tesztelni, az alábbi módon járhatunk el:
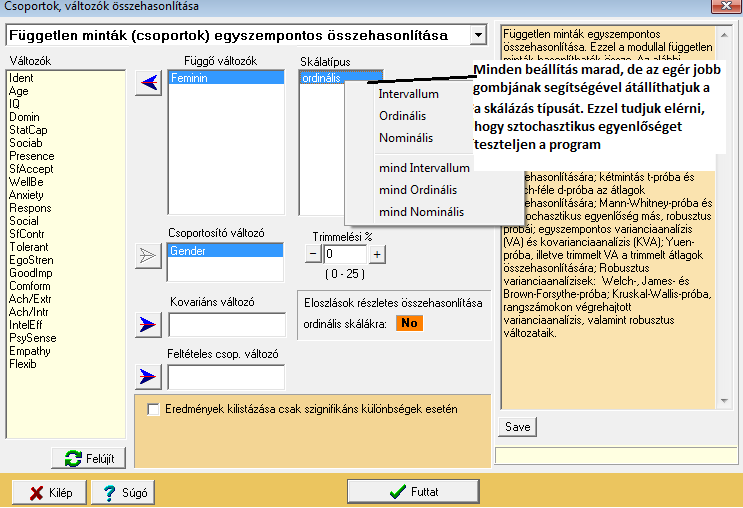
Így az output nyilván megváltozik:
A beolvasott összes eset száma: 94
Csoportosító változó: Gender (Gender of subjects)
Jelölés: +: p < 0,10 *: p < 0,05 **: p < 0,01 ***: p < 0,001
FÜGGŐ VÁLTOZÓ: Feminin (Femininity)
Csoportonkénti alapstatisztikák
|
Index |
Gender |
Esetek | Rang-átalag | Rang-szórás | Min. | Max. |
| 1 | Male | 12 | 26,79 | 26,98 | 8 | 16 |
| 2 | Female | 70 | 44,02 | 22,19 | 10 | 18 |
Elméleti rangszórások egyenlőségének tesztelése
- O'Brien-próba (Welch-féle): F(1,0; 12,8) = 1,306 (p = 0,2741)
- Levene-próba (Welch-féle): F(1; 15,1) = 1,588 (p = 0,2267)
Sztochasztikus egyenlőség tesztelése
Hagyományos eljárás, amely feltételezi a szóráshomogenitást:
- Mann-Whitney-próba (normális közelítés): Z = -2,339 (p = 0,019)*
Szóráshomogenitást nem igénylő robusztus közelítő eljárások:
- Fligner-Policello-próba Welch-féle szabadságfokkal: FPW(11,0) = -2,169 (p = 0,0528)+
- Brunner-Munzel-próba: BM(12,1) = -2,108 (p = 0,0566)+
Pont- és intervallumbecslés a valószínűségi fölény A mutatójára:
A12 = 0,290 [ P(Csop1 > Csop2) = 0,243, P(Csop1 < Csop2) = 0,663 ]
C(0,95) = (0,073; 0,507)
Ebben az esetben úgy lehet a hipotézist felfogni, hogy ha találomra választanánk egy férfit és egy nőt, akkor melyiknek lenne a feminitás-skálán mért értéke várhatóan a nagyobb. Ezt kívánjuk tesztelni.
Ehhez először ugyanúgy a létszámon és a csoportosító változón, majd a jelöléseken kell végigmenni. Ezek után következnek a leíró statisztikák. Azonban, miután itt sztochasztikus egyenlőséget tesztelünk, ezért ezek rangsorolásos eljárások, ahol a rangszámok átlagai és szórásai kerülnek górcső alá.
A „hagyományos” rangsorolásos eljáráshoz nem kell a normalitás (éppen azért szoktuk ezt az esetet vizsgálni, mert a normalitás sérül az eredeti változónknál), viszont a rangsorok szórásának egyenlősége itt is feltétel lesz. Ezt ugyanúgy teszteljük, mint a rendes esetben – tehát, ha itt *-ot jelez valamely próba (Levene, O’Brien), akkor a robusztus alternatívát kell figyelnünk.
Ezek után jön a hagyományos, Mann-Whitney-féle eljárás (hivatkozni a Z-értékre és a p-értékre kell). Itt azt láthatjuk, hogy szignifikáns eltérés van a rangátlagok között.
Amennyiben a szóráshomogenitás sérül, úgy a FPW-próba (a hozzá tartozó statisztikával és p-értékkel), vagy a BM-próba (szintén a hozzá tartozó statisztikával és p-értékkel) lesz az irányadó.
Ezen kívül az előző blokkban megismert előjelpróba általánosítása is szerepet kaphat, az úgynevezett valószínűségi fölény mutatója, melynek segítségével értelmezhetőek, magyarázhatóak, interpretálhatóak az előző eredmények: mennyi annak a várható valószínűsége, hogy az első vagy a második csoport „nyer”, azaz hogy valamely csoport nagyobb értéket ér el.
Minden tesztünk azt mutatja, hogy a férfiak alacsonyabb feminitás-értékekkel rendelkeznek, mint a nők.
Egy változó nagyságszintjének tesztelése 2 csoportban – az SPSS programcsomagban
Az SPSS-ben tehát csak a kétmintás t-próbával, illetve a Mann–Whitney-próbával fogunk megismerkedni, a többi rangstatisztikai módszert nem fogjuk alkalmazni. Továbbá a szóráshomogenitást is csak a Levene-próbával fogjuk tesztelni, a normalitás-tesztelésről pedig feltételezzük, hogy előtte elvégeztük, ahogy azt az első fejezetben megismertük.
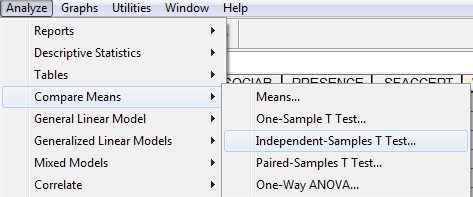
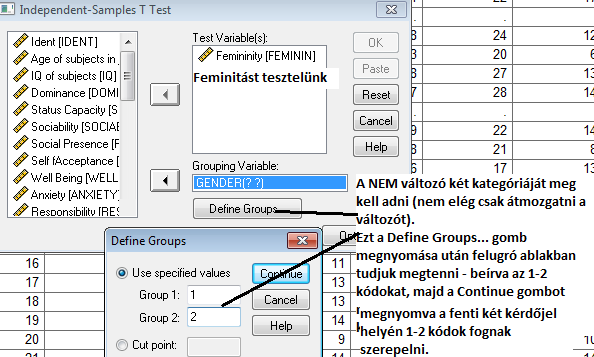
Amennyiben mindent jól csináltunk, úgy a kétmintás t-próba outputját nyerjük:
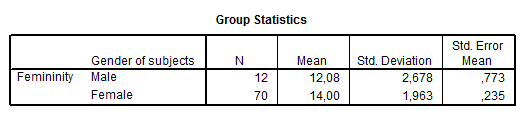
Az első táblázatban a leíró statisztikák láthatóak csoportonként.
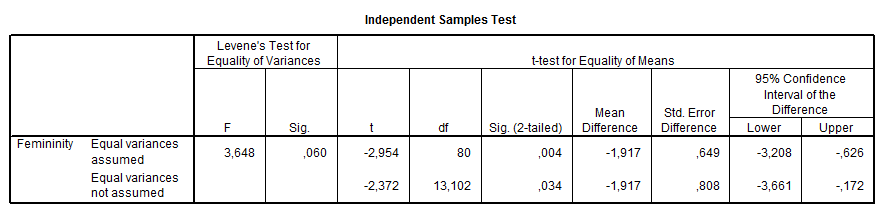
A második táblázatnak két sora van: hogy a két sor közül melyiket használjuk, az első két érdemi oszlopban található Levene-próba fogja eldönteni. Az első sor ugyanis a hagyományos kétmintás t-próba statisztikáit tartalmazza, míg a második sor a Welch-féle d-próba eredményeit. Tehát, ha a Levene-próba második oszlopában látható Sig.-érték 0,05 alá kerül (most felette van), akkor az azt jelenti, hogy a két szórás szignifikánsan eltér egymástól, tehát nem használható a t-próba (azaz ekkor kell a második sort választani).
Most a Sig.-érték 0,05 feletti, tehát az első sorból kiolvassuk a t-értéket (-2,954), szabadsági fokot (80) és Sig.-értéket (0,004). Ezek alapján elmondható, hogy a férfiak átlaga szignifikánsan alacsonyabb, mint a nők átlaga (az átlagokat az első táblázatban láthatjuk).
Amennyiben mégis szükségessé válik a rangstatisztikák használata, úgy a következő módon járhatunk el:
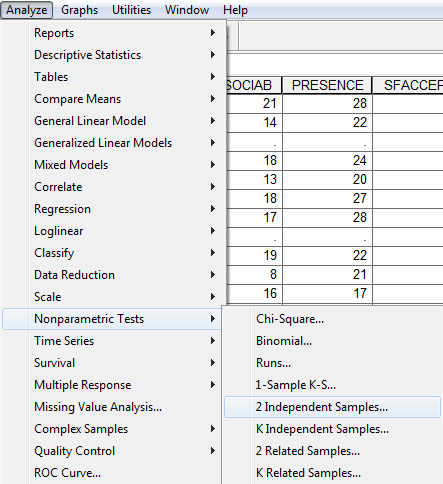
Amennyiben minden beállításunk helyes, az alábbi outputhoz juthatunk:
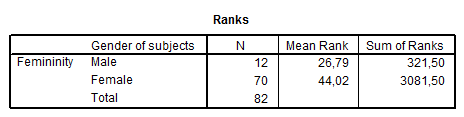
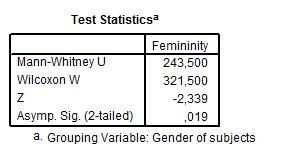
Az első táblázatban a rangstatisztikai értékeket láthatjuk, majd a második táblázatban a Mann–Whitney-statisztika megfelelő értékeit nézhetjük meg (megegyeznek a ROPstat eredményeivel).
Műhelymunkabeli megfogalmazás
A feminitás-változó nemenkénti összehasonlítása – átlag alapján
A feminitás-változó eloszlása nem különbözik szignifikánsan a normálistól (ferdeség és csúcsosság alapján), illetve a két nem esetén számított tapasztalati szórások alapján a két csoport szórása sem tekinthető szignifikánsan különbözőnek (Levene-próba: F(1; 14,6) = 3,409 (p = 0,0852)).
Ennek következtében a hagyományos kétmintás t-próba feltételei fennállnak, így (t(80) = -2,954 (p = 0,0041)) mellett állíthatjuk, hogy a férfiak feminitás-skálán várható átlaga szignifikánsan alacsonyabb, mint a nők feminitás-skálán várható átlaga.
Ha a normalitás sérül, úgy a robusztus tesztek kellenek, majd azokból is azokat kell kiválasztani, melyeket a szórások egyenlőségének tesztelése mutat. Ezeket az elágazásokat egyénileg kell végignézni – a fenti levezetések alapján.
A dolgozatokban tehát a változó ELOSZLÁSA dönti el, hogy a kétmintás tesztek közül az átlagokat vagy a rangsorokat szeretnénk tesztelni (átlagok egyenlősége vagy sztochasztikus egyenlőség lesz a kérdés). Ezek után a megfelelő tesztek közül a szóráshomogenitás fennállása vagy elvetése alapján kell kiválasztani a megfelelőt. Hivatkozásként az alábbiakat tudjuk megfogalmazni szabályként:
- A Levene- / O’Brien-próbáknál az F(szabadsági fok1; szabadsági fok2)-érték és p-érték.
- T-próba, illetve annak robusztus változata (Welch-d) esetén a t-érték, szabadsági fok és a p-érték.
- Mann–Whitney-próba esetén mindenképpen szerepeljen, hogy ekkor már sztochasztikus egyenlőséget tesztelünk, a hivatkozásban z-érték és p-érték kell.
- Az FPW és BM esetén a megfelelő értékek szabadsági fokokkal és p-értékek kellenek.
A több lehetséges elágazás miatt nagyon körültekintőnek kell lenni ezeknél a teszteknél. Vegyük észre azt is, hogy ilyenkor nem biztos, hogy minden eredményt össze tudunk egy táblázatba foglalni, tehát általában szöveges értékeléseket adunk – és az esetleges táblázatokat mellékletbe fogjuk összefoglalni, amennyiben szükséges.