3.5. Két összetartozó minta tesztelése– ROPstat programcsomagban

3.5. Két összetartozó minta tesztelése– ROPstat programcsomagban

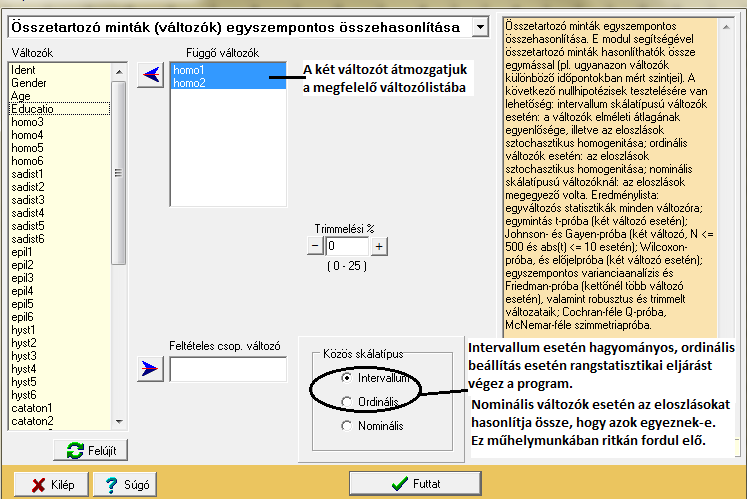
Amennyiben mindent jól állítottunk be, úgy egy már (tartalmában) ismerős outputot kapunk:
Összetartozó minták egyszempontos összehasonlítása
FÜGGÓ VÁLTOZÓK:
homo1
homo2
A beolvasott összes eset száma: 277
Érvényes (komplett) esetek száma: 277
Jelölés: +: p < 0,10 *: p < 0,05 **: p < 0,01 ***: p < 0,001
Elméleti átlagok egyenlőségének tesztelése:
- Egymintás t-próba: t(276) = 1,911 (p = 0,0570)+
- Johnson-próba: J(276) = 1,912 (p = 0,0569)+
- Gayen-próba szignifikanciája: p = 0,0570+
A "Nincs X-ről Y-ra változás" hipotézis vizsgálata:
- Wilcoxon-próba: R+ = 11045,0, R- = 8065,0, z = 1,929 (p = 0,0538)+
"A két változó sztochasztikusan ugyanakkora" hipotézis vizsgálata:
- Előjelpróba: #(X < Y) = 108, #(X > Y) = 87, z = 1,432 (p = 0,1521)
| Index | Változó | Átlag | Szórás | Rangátlag |
| X: | homo1 | 1,809 | 1,232 | 1,46 |
| Y: | homo2 | 1,993 | 1,116 | 1,54 |
| Y - X: | 0,184 | 1,603 |
Ferdeség- és csúcsosságérték és normalitásvizsgálat
Az Y - X változó mintabeli ferdesége = 0,010 (p = 0,946)
Az Y - X változó mintabeli csúcsossága (g4 = a4 - 3) = -0,312 (p = 0,289)
95%-os konfidencia-intervallum az Y-X különbség elméleti átlagára C(0,95) = (-0,005; 0,373)
Pontbecslés a valószínűségi fölény A(Y, X) mutatójára:
A(Y, X)^ = 0,538 ( (X < Y)% = 39,0 (Y = X)% = 29,6 (X > Y)% = 31,4 )
95%-os konfidencia-intervallum A(Y, X)-re: C(0,95) = (0,489; 0,587)
Mint azt már említettük, ebben az esetben lényegében a különbségváltozó 0 voltát teszteljük, így elemeiben az egymintás t-próba elemeit kell viszontlátnunk – és ebben az esetben NEM KELL külön az ordinális esetet futtatni, mert AUTOMATIKUSAN szerepel az outputon a Wilcoxon-próba és az előjelpróba.
Mégegyszer vegyük végig tehát az egymintás t-próbának és robusztus változatainak eseteit: mind a t-próba, mind annak robusztus próbája (Johnson, Gayen) azt mutatja, hogy az eltérés a két változó között tendencia-szintű, tehát nincsen szignifikáns eltérés a homo1 és homo2 kép kedveltsége között.
A Wilcoxon-próba z-értéke és p-értéke szintén hasonlót mutat: tendencia-szintű eltérést tapasztal, azonban ennél több nem mondható el.
Az előjelpróba hasonló eredményre vezet, bár itt már tendencia-szintű különbséget sem tudunk kimutatni.
A próba feltételeinek ellenőrzése az output közepén kapott helyett: a különbségváltozó normalitásának tesztelése ferdeség és csúcsosság alapján azt mutatja, hogy a különbségváltozó ezen 277 fős minta alapján nem különbözik szignifikánsan a normálistól.
Így megállapíthatjuk, hogy a hagyományos egymintás t-próba eredménye (melynek az itteni megnevezése összetartozó mintás t-próba) teljesen megfelel számunkra, bár a többi eredmény is értelmezhető. Mindenesetre megállapítható, hogy a homo1 és homo2 kép kedveltsége szignifikánsan nem tér el egymástól.
Műhelymunkabeli megfogalmazás
Ebben az esetben azonosan hivatkozunk az egymintás t-próba eseteihez, azonban a megfogalmazás más lesz.
Homo1 és homo2 kép kedveltségének összehasonlítása
A két képet egyaránt értékelő 277 esetet figyelembe véve megállapítható összetartozó mintás t-próbával, hogy a két kép kedveltsége szignifikánsan nem különbözik egymástól (t(276) = 1,911, p = 0,057), bár tendencia-szintű eltérés megállapítható, a leíró statisztikák alapján a második kép magasabb pontszámokat mutatott.
A próba feltételét ellenőriztük, a különbségváltozó normalitása a számított ferdeség- és csúcsosság-paraméterek alapján feltételezhető, így a robusztus eljárásokra nem volt szükség.