2.2. FOLYTONOS VÁLTOZÓK ESETE – a KOR-változó bemutatása

2.2. FOLYTONOS VÁLTOZÓK ESETE – a KOR-változó bemutatása
Folytonos változó lehet pl. a kor, testmagasság, testsúly – ezek bemutatására általában a leíró statisztikák közül a változó paramétereinek értékeit alkalmazzuk. Ilyenek az átlag, medián, szórás, variancia, ferdeség – és itt alkalmazhatunk gyakorisági diagramot vagy hisztogramot, melyről például előzetes képet kaphatunk a változónk normalitását illetően.
Folytonos változók esetén itt szokás megtenni az első hipotéziseket is, nevezetesen: azokat a hipotéziseket, melyek a vizsgált változó normalitását hivatottak eldönteni. Erre vonatkozóan mind az SPSS-ben, mind a ROPstat-ban több teszt is van – ezt egy külön fejezetben fogjuk tárgyalni.
A vizsgálat lépései – ROPstat-ban
Két lépésben fogjuk végrehajtani az elemzést, ugyanis mind az alap, mind a részletes mintastatisztikákra szükségünk lehet egy műhelymunka során – és mindkettő leíró statisztikának minősül. Ráadásul a részletes mintastatisztikák automatikusan tartalmaznak egy normalitás-vizsgálati eljárást is, így megint csak időt takarítunk meg magunknak, ha azt használjuk.
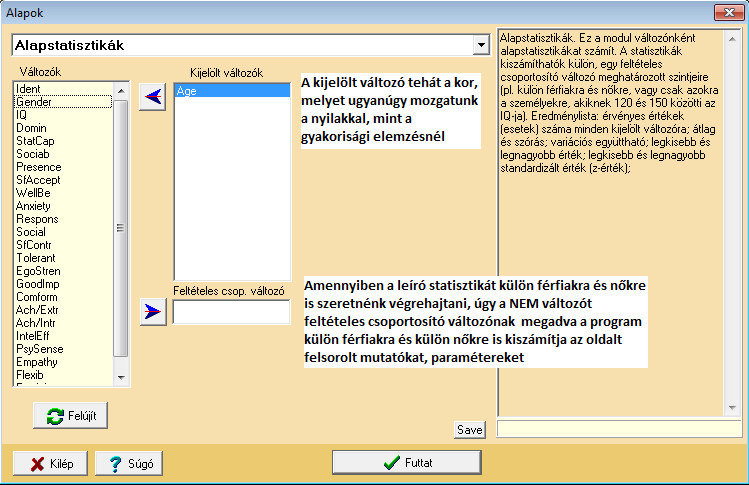
Amennyiben mindkét elemzést lefuttatjuk, ezt a két outputot nyerjük:
Alapstatisztikák
Jelölés:
- Var. eh. = Variációs együttható = Relatív szórás = szórás/átlag
- X_min = Talált legkisebb érték
- X_max = Talált legnagyobb érték
- z_min = Standardizált legkisebb érték = (X_min - átlag)/szórás
- z_max = Standardizált legnagyobb érték = (X_max - átlag)/szórás
A beolvasott összes eset száma: 94
| Index | Változó | Esetek | Átlag | Szórás | Var. eh. | X_min | X_max | z_min | z_max |
| 3 | Age | 94 | 22,59 | 5,808 | 0,257 | 18 | 41 | -0,79 | 3,17 |
________________________________________________________
Az input fájl neve: C:\_vargha\ropstat\dat\CPI.msw
Részletes leíró statisztikák
A beolvasott összes eset száma: 94
| Index | Változó | Esetek | Medián | Átlag | St.hiba | 95%-os | konf.int. | Ferdeség | Csúcsosság |
| 3 | Age | 94 | 20 | 22,59 | 0,599 | 21,39 | 23,78 | 1,316*** | 0,708 |
Jelölés a normalitás tesztelésénél a Ferdeség és a Csúcsosság segítségével: *: p < 0,05 **: p < 0,01 ***: p < 0,001
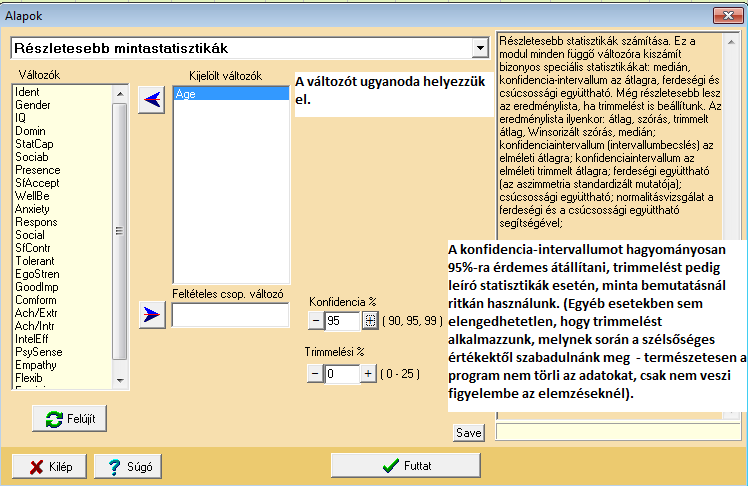
Az alapstatisztikák esetén tehát átlagot, szórást, variációs együtthatót (szórás / átlag, azaz mekkora a szórás az átlaghoz képest), a változó minimális és maximális értékét, illetve a minimum és a maximum standardizált értékét nyerjük (ez utóbbi kettő azt mutatja meg, hogy a legnagyobb és legkisebb érték hány szórásnyira helyezkedik el az átlagtól). Esetünkben jól látható, hogy míg a minimum még 1 szórásnyira sincsen, addig a maximum több mint 3 szórásnyira van. Tehát az eloszlásunk közel sem tűnik szimmetrikusnak – az előző gyakorisági elemzéssel kérhetünk hisztogramot is – a következőkben ennek módját ismertetem.
A részletes leíró statisztikákban az átlag mellett a medián is megjelenik, illetve az átlag standard hibája és a segítségével számított, átlaghoz tartozó 95%-os konfidencia-intervallum (ebben az intervallumban található a populációbeli átlag 95%-os valószínűséggel). A ferdeség és a csúcsosság melletti ***-ok jelzik, ha a változó szignifikánsan eltér a normálistól. Esetünkben is leolvasható a ferdeség melletti ***-ból, hogy az eloszlás lényegesen ferdébb annál, mint amit egy normális eloszlásnál még tolerálni tudunk, tehát a Kor-változó ebben a mintában nagy valószínűséggel nem normális eloszlású.
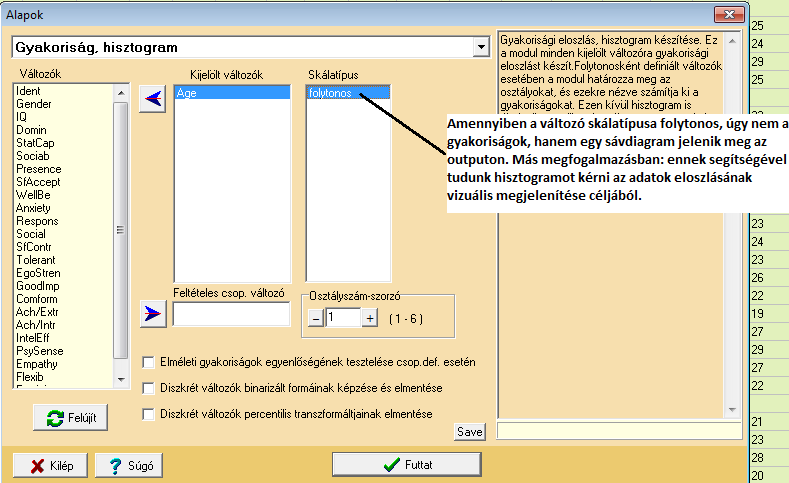
Gyakoriság, hisztogram
A beolvasott összes eset száma: 94
VÁLTOZÓ: Age (Age of subjects in years)
| Oszt.köz | Gyak | % | Kum% | |
| 19,15 | 57 | 60,6 | 60,6 | |============================================ |
| 21,45 | 6 | 6,4 | 67,0 | |==== |
| 23,75 | 2 | 2,1 | 69,1 | |= |
| 26,05 | 8 | 8,5 | 77,7 | |===== |
| 28,35 | 6 | 6,4 | 84,0 | |==== |
| 30,65 | 5 | 5,3 | 89,4 | |=== |
| 32,95 | 3 | 3,2 | 92,6 | |= |
| 35,25 | 4 | 4,3 | 96,8 | |== |
| 37,55 | 2 | 2,1 | 98,9 | |= |
| 39,85 | 1 | 1,1 | 100,0 | | |
| Össz: | 94 | |||
Jól látható, hogy az eloszlásunk valóban igen ferde a normális eloszlás görbéjéhez képest – az alsó régiók igen-igen túlreprezentáltak a felsőbb korkategóriák rovására. A program saját maga készít kategóriákat, melyekbe a kor alapján elhelyezi a vizsgálati alanyokat.
A vizsgálat lépései – SPSS-ben
Az SPSS-ben a fenti adatok közül néhányat nem fogunk tudni megjeleníteni, illetve néhány számítás kell hozzá, hogy a ROPstat-tal azonos információkat kiolvashassuk ebből a programból is.
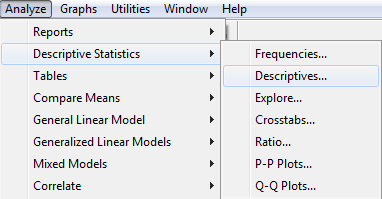
Az SPSS-ben csak egy menüpontot használunk, azon belül tudunk elérni minden lehetséges értéket – azonban figyeljünk oda, hogy itt az adattartalom el fog térni a ROPstat adattartalmához képest!
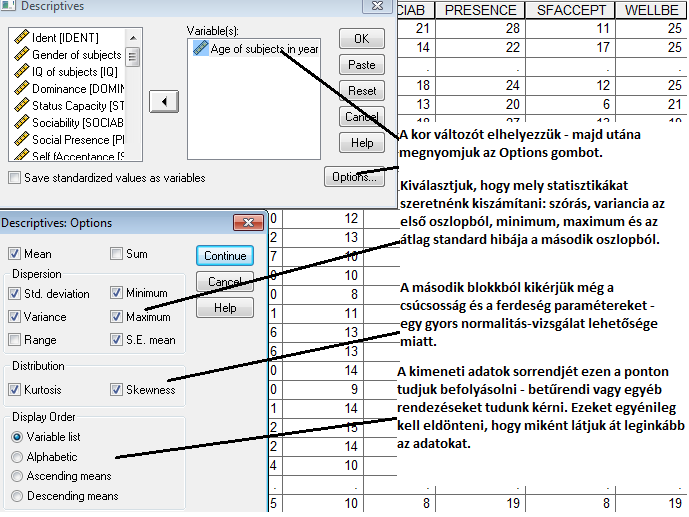
A megfelelő beállítások alkalmazása után az alábbi outputot kapjuk:

Általános eljárásként elmondható, hogy egy paraméter 95%-os konfidencia-intervallumát az alábbi eljárással kaphatjuk meg:
Az intervallum alsó határa: paraméter – 2x(standard hiba)
Az intervallum felső határa: paraméter + 2x(standard hiba)
PÉLDA:
A ferdeség és csúcsosság esetén:
A ferdeség 95%-os konfidencia-intervallumának alsó határa: 1,3 – 2 x 0,25 = 0,8
A ferdeség 95%-os konfidencia-intervallumának felső határa: 1,3 + 2 x 0,25 = 1,8
A csúcsosság 95%-os konfidencia-intervallumának alsó határa: 0,7 – 2 x 0,5 = -0,3
A csúcsosság 95%-os konfidencia-intervallumának felső határa: 0,7 + 2 x 0,5 = 1,7
Így megállapíthatjuk, hogy a ferdeség esetén a 0 nincsen benne a 95%-os konfidencia-intervallumban, míg a csúcsosság esetén igen – tehát az eloszlás szignifikánsan ferdébb, mint a normális eloszlás, azonban a csúcsossága nem különbözik tőle szignifikánsan. Ezzel együtt azonban megállapítható, hogy a KOR-változó eloszlása szignifikánsan nem normális.
A többi paraméter már kiolvasható a táblázatból.
Fontos azonban észrevenni, hogy a Variance (variancia, szórásnégyzet) oszlopot megelőző paraméter kiírása nem történt meg. Az Std. felirat az Std. deviation (szórás) paramétert takarja.
Normalitás-vizsgálat – mindkét programban
A normalitásra tehát már megfogalmazhattunk egy megállapítást a ferdeség alapján, hiszen a programok azt mutatták, hogy a KOR-változó eloszlása szignifikánsan különbözik a normális eloszlástól.
A két programban azonban van lehetőségünk arra, hogy külön, bármely változóra normalitás-vizsgálatot kérjünk. Erre vonatkozóan 3 módszerünk lesz:
- A ferdeség és csúcsosság alapján egy paraméteres teszt, mely
esetén azt teszteljük, hogy a vizsgált változónk említett két
paramétere szignifikánsan különbözik-e a normális eloszlás 0-0
ferdeség-csúcsosság értékétől. Ezt úgy tesszük meg, hogy:
- A ROPstat program automatikusan kiszámítja helyettünk a konfidencia-intervallumot és megjelöli számunkra, ha valamely érték szignifikáns eltérést mutat a hipotetikus 0 értéktől.
- Az SPSS-ben a ferdeség és csúcsosság mellé egy-egy standard hibát számít a program, melyek nagyjából 2-szeresét hozzáadva és kivonva a számított paraméterből meghatározhatjuk a ferdeség és csúcsosság konfidencia-intervallumait. Ezek után, ha ezek az intervallumok tartalmazzák a 0-t, akkor nincsen szignifikáns eltérés – ha nem tartalmazzák, akkor a változó eloszlása szignifikánsan eltér a normális eloszlástól.
- A folytonos változók illeszkedés-vizsgálatának egyik legrégibb, általános módszere a Kolmogorov, vagy Kolmogorov–Szmirnov-eljárás. Az SPSS-ben ezt az eljárást használjuk általában normalitás tesztelésére. A ROPstat bizonyos esetszám alatt ezt, bizonyos esetszám felett a 3. pontban ismertetett eljárást választja.
- A harmadik lehetőség a diszkrét változókra használható khi-négyzet statisztika, mely azonban használható folytonos eloszlások esetén is – ilyen helyzetben diszkretizálunk, csoportokat hozunk létre. Ezt a ROPstat megteszi helyettünk (az SPSS nem, így ezt nem is használjuk), tehát itt is csak az eredményt kell értelmeznünk. Fontos megjegyezni, hogy ehhez a statisztikához (is) nagyobb elemszám szükséges, tehát kisebb mintánál nem ezt fogjuk találni a ROPstat esetén sem.
A ferdeség és csúcsosság segítségével végzett elemzést már megnéztük. A khi-négyzet statisztikát csak a ROPstat programban fogjuk elérni (az SPSS-ben ennek alkalmazása egyéb technikákat is igényel).
Normalitás-vizsgálat ROPstat-ban
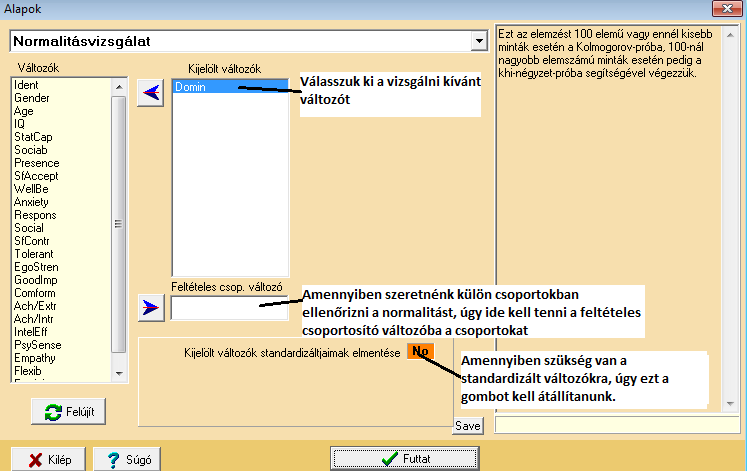
E fenti beállításokkal az alábbi output születik:
Az input fájl neve: C:\_vargha\ropstat\dat\CPI.msw
Normalitásvizsgálat (a normális eloszlás nullhipotézisének tesztelése)
A beolvasott összes eset száma: 94
Jelölés: +: p < 0,10 *: p < 0,05 **: p < 0,01 ***: p < 0,001
VÁLTOZÓ: Domin (Dominance)
Érvényes értékek száma: 82
Kolmogorov-féle normalitásvizsgálat: Dmax = 0,089, D* = 0,808 (p = 0,5318)
Látható, hogy a Kolmogorov-féle vizsgálatot hajtotta végre a program (a HELP-ben ezt meg is nézhetjük, hogy a khi-négyzet statisztikához legalább 100 fős mintára van szükség).
A dominancia-változó ezek alapján, p = 0,5318-as érték mellett, nem különbözik szignifikánsan a normálistól.
Normalitás-vizsgálat SPSS-ben
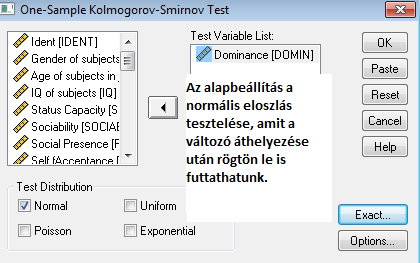
Az SPSS-ben tehát csak Kolmogorov-féle megoldást fogunk választani, mely az alábbi menüpontban található:
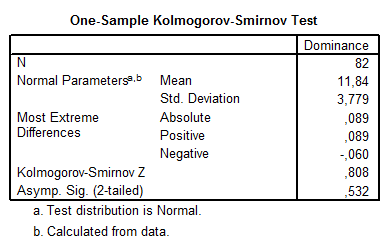
Amennyiben jól helyeztünk el mindent, úgy az alábbi outputot kapjuk:
Megfigyelhető, hogy a paraméterek ugyanazok: a Z-statisztika értéke (mely a ROPstatban D*-ként szerepelt) 0,808, a hozzá tartozó Asymp. Sig (mely a ROPstatban „p”) 0,532.
Így megállapítható, hogy a ROPstattal azonos eredmény született, a dominancia-változó az SPSS számításai alapján sem különbözik szignifikáns módon a normálistól.
Fontos kiemelni, hogy szándékosan nem a KOR-változóval végeztem el ezt a vizsgálatot, mert onnan már a részletes statisztikáknál kaptunk információt. Ez a vizsgálat általában azoknál a változóknál érdekes, melyekre később hipotéziseket készülünk építeni (a KOR-változó nem feltétlenül ilyen). A felvett kérdőívek skálái, összesített eredményei szoktak olyan szerepet betölteni, hogy esetükben fontos lehet a normalitás ellenőrzése.
Műhelymunkabeli megfogalmazás
Ebben az esetben több mindent kell összefoglalnunk néhány mondatban, több eredményünket kell tömör formában ismertetnünk. Ismertetnünk kell ugyanis a számunkra fontos paramétereket, illetve a normalitásról is ejthetünk itt pár szót.
A KOR-változó ismertetése
A mintába kerültek átlagéletkora 22,6 év volt, szórása 5,8 év. A minta eloszlása ferde: a fiatalabbak lényegesen nagyobb arányban reprezentáltak, mint az idősebbek, ezt támasztja alá a standardizált minimum és maximum érték (-0,79 és 3,17), továbbá az eloszlás ferdesége is (1,316) – azaz a maximális érték lényegesen távolabb van az átlagtól, mint a minimális érték.
A normalitás kérdése:
A DOMINANCIA-változó normalitására vonatkozó megfogalmazás – ROPstat használata esetén
A dominancia-változó normalitását Kolmogorov-teszttel ellenőriztük (D* = 0,808, p = 0,5318), és azt mondhatjuk, hogy a dominancia-változó eloszlása nem különbözik szignifikánsan a normálistól.
A DOMINANCIA-változó normalitására vonatkozó megfogalmazás – SPSS használata esetén
A dominancia-változó normalitását Kolmogorov-teszttel ellenőriztük (z = 0,808, Asymp. Sig = 0,532), és azt mondhatjuk, hogy a dominancia-változó eloszlása nem különbözik szignifikánsan a normálistól.
Amennyiben SPSS programot használunk, úgy a folytonos változók előzetes bemutatására a Kolmogorov-teszttel időt takaríthatunk meg, hiszen az általánosan használt paraméterek szerepelnek a statisztika outputján. Így az SPSS használata esetén a dominancia-változó bemutatása a következő megfogalmazásban is történhet:
A dominancia-változót 82 vizsgálati személy esetén tudtuk meghatározni: a minta átlaga 11,84 lett, szórása 3,78. A változó normalitását Kolmogorov-teszttel ellenőriztük (z = 0,808, Asymp. Sig = 0,532), és azt mondhatjuk, hogy az eloszlása 95%-os szinten normálisnak tekinthető.
Megjegyzések
E fenti adatokat is össze lehet foglalni (amennyiben több változó is vizsgálatra kerül) táblázatos formában, nem kell mindegyik változóra e fenti, szöveges megfogalmazást alkalmazni. A lényeg, hogy a megfelelő hivatkozási értékek (statisztikai érték, szignifikancia) feltüntetésre kerüljenek.
Fontos tehát kiemelni: MINDEN OLYAN ESETBEN, ahol STATISZTIKAI ÁLLÍTÁS történik, az alkalmazott statisztikai eljárásban számított STATISZTIKAI ÉRTÉK, ha van SZABADSÁGI FOKA és SZIGNIFIKANCIA SZINTJE, KÖTELEZŐEN FELTÜNTETENDŐ ÉRTÉK!