3.3. Egy változó nagyságszintjét szeretnénk tesztelni legalább 3 csoportban

3.3. Egy változó nagyságszintjét szeretnénk tesztelni legalább 3
csoportban
Ebben a fejezetben olyan kérdéseket tárgyalunk, amikor legalább 3 csoport kerül összehasonlításra valamely vizsgált változó mentén. (Hasonló az előző fejezethez, csak több csoporttal). A kérdésfelvetés szakmailag többek között az alábbi módon fogalmazható meg:
- Igaz-e, hogy ha az IQ-változó alapján 3 kategóriát hozunk létre, akkor az IQ emelkedésével együtt jár a feminitás-érték növekedése?
Ismét olyan hipotézist fogalmaztunk meg, mely nem egészen a statisztikai hipotézis – hiszen nem egyenlőség, hanem eltérés szerepel benne. A statisztikai hipotézis, melyet vizsgálni tudunk:
- Igaz-e, hogy ha az IQ-változó alapján 3 kategóriát hozunk létre, akkor az IQ emelkedése nem befolyásolja a feminitás várható értékét?
Ezt már tudjuk kezelni statisztikailag. Matematikailag az előző blokk általánosítása történik hagyományos esetben. Sztochasztikus homogenitás / egyenlőség esetén nem triviális az általánosítás, így itt némi többlet végiggondolásra lesz szükségünk. A hagyományos eljárásban továbbra is feltétel lesz a normalitás és a szóráshomogenitás (a hagyományos eljárás itt a varianciaanalízis, vagy VA vagy ANOVA).
A normalitás sérülése esetén alkalmazott rangstatisztikai eljárások során használt sztochasztikus homogenitás azonban egy érdekes sajátosságot hordoz a hagyományos módszerrel szemben: ha a hagyományos módszerben az átlagokat összehasonlítjuk, akkor igaz lesz az alábbi:
- Ha A csoport átlaga nagyobb, mint B csoport átlaga, mely nagyobb, mint C csoport átlaga, akkor ebből következik, hogy A csoport átlaga nagyobb, mint C csoport átlaga. Ilyen esetben tehát a PÁRONKÉNTI eltérések egyértelmű sorrendet határoznak meg. A páronkénti eredmények egyértelmű rangsort is definiálnak a csoportok között.
Azonban sztochasztikus homogenitás esetén ez bonyolultabb. Eddig is úgy próbáltuk meg kezelni a sztochasztikus fölényt, hogy ha egyik vagy másik csoportból kivennénk 1-1 egyedet, és versenyeztetnénk, akkor valamely csapat szisztematikusan legyőzné-e a másik csapatot. Azonban ebben az esetben a legkönnyebb a sportból vett „körbeverés” esetét felidézni: A mindig megveri B-t, B mindig megveri C-t, de C mindig megveri A-t. Tehát, bár PÁRONKÉNT mindig van domináns csoport, összességében mégsem mondhatunk senkit dominánsnak. Ez lesz a rangstatisztikák egyik érdekessége ebben az esetben: itt akkor mondunk majd valakit sztochasztikusan dominánsnak, ha MINDENKIT meg tud verni.
Egy változó nagyságszintjének tesztelése legalább 3 csoportban – ROPstat programcsomagban
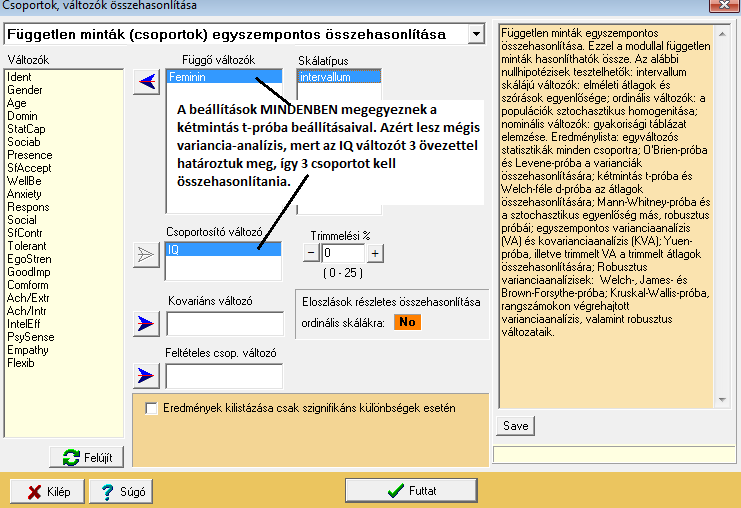
Ha minden beállítás megegyezik a fentivel, ezt az outputot nyerjük:
Független minták egyszempontos összehasonlítása
A beolvasott összes eset száma: 94
Csoportosító változó: IQ (IQ of subjects)
Jelölés: +: p < 0,10 *: p < 0,05 **: p < 0,01 ***: p < 0,001
FÜGGŐ VÁLTOZÓ: Feminin (Femininity)
Csoportonkénti alapstatisztikák
| Index | IQ | Esetek | Átlag | Szórás | Min. | Max. | Ferdeség | Csúcsosság |
| 1 | low | 22 | 13,59 | 2,282 | 10 | 18 | 0,188 | -0,897 |
| 2 | middle | 36 | 13,61 | 2,032 | 8 | 17 | -0,689+ | 0,416 |
| 3 | high | 24 | 14,00 | 2,341 | 10 | 18 | 0,155 | -0,556 |
Ha a Ferdeség vagy a Csúcsosság szignifikáns, az a normalitás sérülését jelzi.
Elméleti szórások egyenlőségének tesztelése
- O'Brien-próba (Welch-féle): F(2,0; 48,2) = 0,384 (p = 0,6830)
- Levene-próba (Welch-féle): F(2; 47,5) = 0,642 (p = 0,5306)
Elméleti átlagok egyenlőségének tesztelése
Hagyományos eljárás, amely feltételezi a szóráshomogenitást:
- Varianciaanalízis: F(2; 79) = 0,278 (p = 0,7579)
Hatásvariancia = 1,3375, Hibavariancia = 4,8085
Korrelációs hányados (nemlineáris korrelációs együttható): eta = 0,084
Megmagyarázott variancia-arány: eta-négyzet = 0,007
Robusztus eljárások, amelyeknél nem szükséges a szóráshomogenitás:
- Robusztus Welch-féle varianciaanalízis: W(2; 45,6) = 0,253 (p = 0,7777)
- James-próba: U = 0,513 (p > 0,10)
- Brown-Forsythe-próba: BF(2; 67) = 0,267 (p = 0,7661)
Az (ANO)VA-elemzésnél a normalitás vizsgálata a ferdeség és csúcsosság paraméterek segítségével történik – látható, hogy egyik csoportban sem sérül a normalitás. Szintén ebben a táblázatban láthatók az átlagok, szórások, esetszámok.
A próba másik feltétele a szórások egyezése. Ennek megszokott próbáit láthatjuk a következő blokkban, ahonnan leolvashatjuk, hogy a csoportok szórásai szignifikánsan nem különböznek egymástól.
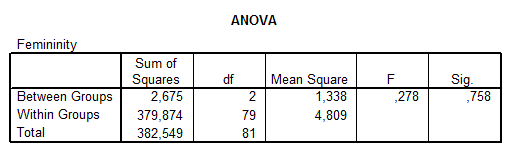
Az átlagok összehasonlítása megtörténik, a páros összehasonlításokat viszont azért nem látjuk, mert a kapott eredmények alapján nincsenek szignifikáns eltérések a csoportok között. Ezt az első sorban lévő varianciaanalízis-értékből tudjuk kiolvasni – a hozzá tartozó p-érték elég magas, tehát a feminitás nem mutat eltérést a különböző IQ-kategóriákban.
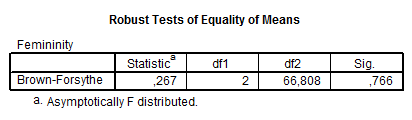
Amennyiben nem teljesülne a szóráshomogenitás feltétele, úgy a következő blokkban tudnánk a megfelelő varianciaanalízis-statisztikákat kiolvasni, innen általában a Brown–Forsythe-próbát szokás használni. A robusztus tesztek szintén azt mutatják, hogy nincsenek szignifikáns eltérések.
Amennyiben sérül a normalitás, úgy a következő eljárást kell alkalmazni:
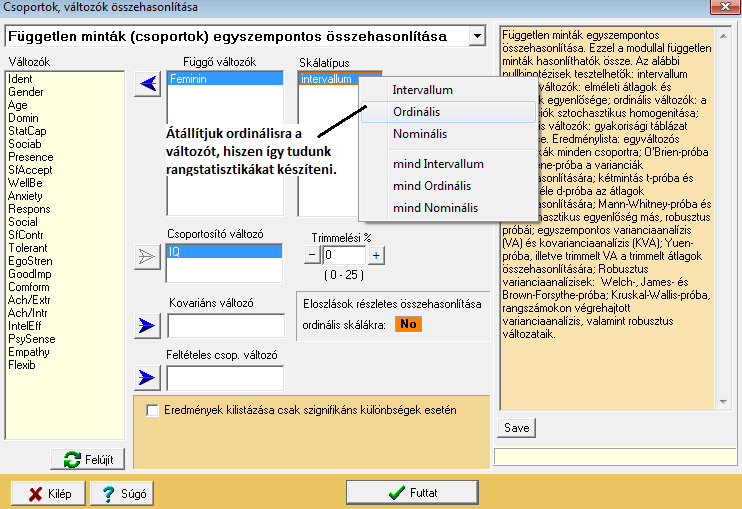
Ekkor az alábbi outputot kapjuk:
Az input fájl neve: C:\_vargha\ropstat\dat\CPI.msw
Független minták egyszempontos összehasonlítása
A beolvasott összes eset száma: 94
Csoportosító változó: IQ (IQ of subjects)
Jelölés: +: p < 0,10 *: p < 0,05 **: p < 0,01 ***: p < 0,001
FÜGGŐ VÁLTOZÓ: Feminin (Femininity)
Csoportonkénti alapstatisztikák
| Sztochasztikus dominancia | ||||||
| Index | IQ | Esetek | Rang-átlag | Rang-szórás | Súlyozott | Nem súlyozott |
| 1 | low | 22 | 39,52 | 25,54 | 0,476 | 0,476 |
| 2 | middle | 36 | 41,28 | 22,00 | 0,497 | 0,498 |
| 3 | high | 24 | 43,65 | 24,83 | 0,526 | 0,526 |
Megjegyzés:
Minden csoport esetében a sztochasztikus dominancia annak a valószínűségét jelzi,
hogy egy random megfigyelés ebből a csoportból (Xj) nagyobb lesz, mint egy random
megfigyelés az egész mintából (X), plusz az egyenlőség valószínűségének a fele:
SZTDj = P(Xj > X) + 0,5P(Xj = X)
A sztochasztikus homogenitás definíciója: SZTD1 = SZTD2 = SZTD3 = ... = 0,50
Elméleti rangszórások egyenlőségének tesztelése
- O'Brien-próba (Welch-féle): F(2,0; 46,1) = 0,866 (p = 0,4275)
- Levene-próba (Welch-féle): F(2; 47,9) = 1,058 (p = 0,3550)
Sztochasztikus homogenitás tesztelése
Hagyományos eljárás, amely feltételezi a szóráshomogenitást:
- Kruskal-Wallis-próba: H(2) = 0,357 (p = 0,8366)
Szóráshomogenitást nem igénylő robusztus közelítő eljárás:
- Korrigált rang Welch-próba: rW3(2; 45,4) = 0,155 (p = 0,8568)
KULLE-féle aszimptotikusan egzakt próbák
- Populációk azonos súlyozása:
Khi2(1,93) = 0,351 (p = 0,8257) F(1,93; 79,0) = 0,182 (p = 0,8261)
- Mintaelemszámokkal arányos súlyozás:
Khi2(1,92) = 0,354 (p = 0,8228) F(1,92; 79,0) = 0,184 (p = 0,8232)
Ebben az esetben a rangátlagokkal kell elsősorban dolgozni – ezeket fogjuk összehasonlítani. Ennek is feltétele a szóráshomogenitás – de itt a rangsorok szórásainak egyenlősége szükséges. Ennek is a szokásos tesztjei láthatóak az első blokkban, melyekből megállapítható, hogy a rangszórások nem különböznek szignifikánsan egymástól.
A sztochasztikus homogenitás hagyományos, szóráshomogenitási feltétel megléte melletti tesztje a Kruskal–Wallis-próba, mely azt mutatja, hogy nincsen sztochasztikusan domináns csoport.
Amennyiben nem állna fent a szóráshomogenitás, úgy a korrigált Welch-próbát kellene figyelnünk (most ez sem jelez eltérést).
Megállapíthatjuk tehát, hogy bármely eljárást nézzük is – átlagok, rangsorok – nem állapítható meg eltérés a feminitás értékeiben az IQ által övezetekre bontott populációban.
Egy változó nagyságszintjének tesztelése legalább 3 csoportban – SPSS programcsomagban
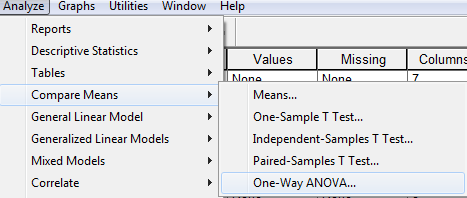
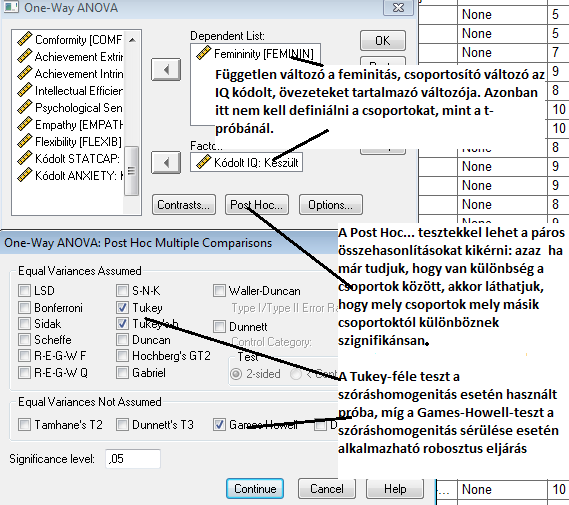
Amennyiben mindent jól állítottunk be, az alábbi outputot nyerjük:
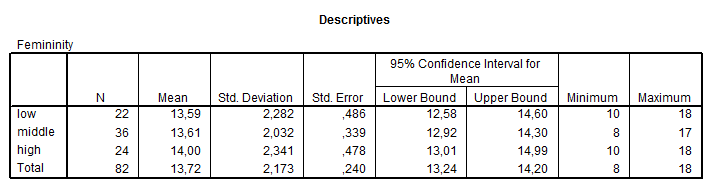

A táblázatok hasonló információkat tartalmaznak, mint a ROPstat esetén. Először itt is a leíró statisztikákkal találkozhatunk. A következő output itt is a szóráshomogenitás – bár az SPSS csak a Levene-tesztet használja.
Az ANOVA-táblázat a hagyományos varianciaanalízis táblája, melyben az F-érték és a Sig.-érték számít – itt is megfigyelhetjük, amit már a ROPstatnál, hogy nem jelez szignifikáns eltéréseket. A hagyományos után a robusztus, szóráshomogenitást nem igénylő Brown–Forsythe-tesztet láthatjuk (ez sem jelez eltérést, bár ezt most úgyis figyelmen kívül hagyjuk).
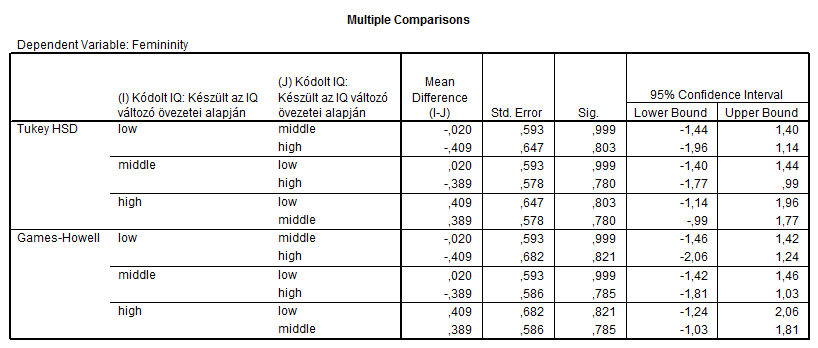
Az első és legnagyobb eltérés a ROPstat és az SPSS között ebben az eljárásban, hogy az SPSS mindenképpen kiszámolja és kiírja a páros összehasonlítások táblázatait – függetlenül attól, hogy vannak-e szignifikáns eltérések vagy sem.
Ezek közül az első táblázatban páronként (egy-egy sorban egy-egy páros összehasonlítása látható) írja ki az eredményeket, ahol az átlagok közötti különbségek, annak standard hibája, illetve az eltérés 0 voltának tesztelési eredménye látható (Sig.-érték). Amennyiben a Sig.-érték 0,05 alá csökken, akkor van a két csoport között szignifikáns eltérés.
A Tukey-féle teszt a szóráshomogenitás megléte mellett értelmezhető, míg a Games–Howell-statisztika robusztus a szóráshomogenitás feltételére nézve.
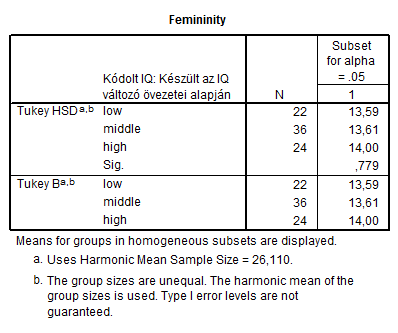
A másik, hasonló tartalommal bíró táblázat az átlagokat csoportosítva jeleníti meg, tehát tömörebb, vizuálisabb formában örökíti meg az eredményeket számunkra.
Amennyiben nem teljesül a normalitás, úgy rangstatisztikai eljárást tudunk alkalmazni, azonban ez nem lesz annyira részletes, mint a ROPstat hasonló rutinja (így azt javasoljuk, hogy amennyiben rangstatisztikai eljárásra van szükségünk, használjuk a ROPstatot).
Amennyiben mindent beállítottunk, az alábbi outputot nyerjük:


A rangstatisztikai eljárás az SPSS-ben lényegesen rövidebb, itt csak a Kruskal–Wallis-teszt látható, illetve az értelmezéshez, interpretációhoz szükséges rangstatisztikai leíró statisztikák. Ez alapján, a benne lévő khi-négyzet statisztika és a hozzá tartozó Asymp. Sig-érték alapján elmondható, hogy, hasonlóan a ROPstat eredményéhez, itt sem láthatunk semmifajta szignifikáns eltérést a rangátlagok között, nincsen szignifikánsan domináns csoport.
Műhelymunkabeli megfogalmazás
E kérdések változatos módokon interpretálhatók egy műhelymunkában, hiszen elég összetett eljárásról van szó – annak ellenére, hogy maga a hipotézis egyszerű, nagyon sok részeljárás van, melyekről mindenképpen kell írni, hogy valid legyen a vizsgálatunk.
A feminitás-változó IQ-övezetek szerinti összehasonlítása
Az IQ-változót 3 övezetre bontottuk (alacsony, közepes és magas), majd e 3 övezetben vizsgáltuk a feminitás-változó nagyságszintjét. Bár a csoportonként kiszámított ferdeségi és csúcsossági mutatók egyike sem mutatott szignifikáns eltérést a normális eloszlás megfelelő paramétereitől, rangstatisztikai eszközökkel is megvizsgáltuk a kérdést.
Azt tapasztaltuk, hogy mind a hagyományos eljáráshoz szükséges szóráshomogenitás fennáll (Levene-próba: F(2; 47,5) = 0,642 (p = 0,5306)), mind a rangstatisztikákhoz szükséges rangsorok szórásának homogenitása teljesül (Welch-féle Levene-próba: F(2; 47,9) = 1,058 (p = 0,3550)). Így az átlagoknak és rangátlagoknak a hagyományos eljárásait alkalmazhattuk.
Az átlagok hagyományos eljárással sem (F(2; 79) = 0,278 (p = 0,7579)), illetve Kruskal–Wallis-féle rang-ANOVA eljárással sem (H(2) = 0,357 (p = 0,8366)) különböznek egymástól szignifikánsan.
Megállapíthatjuk tehát, hogy az IQ növekedő csoportjaiban a feminitás átlaga szignifikánsan nem különbözik egymástól
Fontos észrevenni és megemlíteni, hogy ha páros összehasonlításokat teszünk, akkor azt táblázatos formában vagy akár oszlopdiagramos formában is érdemes lehet ábrázolni (az átlagokat feltüntetve), vagy pontdiagrammal, összekötve az átlagokat, stb. Ezen a ponton már nagyon nagyfokú szabadságunk van, hiszen az eredmények értelmezése, interpretációja változatos lehet. Figyeljünk azonban oda, hogy a szükséges hivatkozások minden esetben pontosan jelenjenek meg a dolgozatban.
- A Levene- / O’Brien-próbáknál az F(szabadsági fok1; szabadsági fok2)-érték és a p-érték.
- ANOVA, illetve annak robusztus változata (Brown–Forsythe) esetén az F-érték, szabadsági fokok és a p-érték.
- Kruskal–Wallis-próba esetén mindenképpen szerepeljen, hogy ekkor már sztochasztikus homogenitást tesztelünk (vagy hogy rangsorokon elemzünk), hivatkozásban H-érték és p-érték kell.
- A páros összehasonlításoknál érdemes lehet táblázatos formában bemutatni az adatokat, akár az eredeti SPSS vagy ROPstat outputtal. Hivatkozni a megfelelő t-értékekre kell, illetve Sig.- vagy p-értékre.
Ne felejtsük el, hogy a ROPstat csak abban az esetben vizsgálja a páros összehasonlításokat, ha a varianciaanalízisben szignifikáns különbséget talál – egyéb esetben ezt az elemét az outputnak nem fogjuk látni. Nyilván, ha nincsenek különbségek, akkor a páros összehasonlítások bemutatása sem lehet kötelező.